電気四重極子ポテンシャル

のぼりんさんの書込 (2008/05/11(Sun) 16:42)

こんにちは．久しぶりに訪問しましたが，今回もよろしくお願いします．

参考書によると，電気量 q の点電荷が (±d/2, 0, 0) に，また電気量 -q の点電荷が (0, ±d/2, 0) に配置されているらしいです（参考書には，厳密な説明がありませんでした）．この電気四重極子の，点 P でのポテンシャルは，P の位置を r として，

$\phi (\bm{r}) & = \frac{q} {4\pi \varepsilon _0 r} \left[ {\frac {1} {\sqrt {1 - {\textstyle{{dx} \over {r^2 }}} + \left( \textstyle{d \over {2r}} \right)^2 } } + \frac{1} {\sqrt {1 + {\textstyle{{dx} \over {r^2 }}} + \left( {\textstyle{d \over {2r}}} \right)^2 } }} \right. \\& \left. - \frac{1} {\sqrt {1 - {\textstyle{{dy} \over {r^2 }}} + \left( {\textstyle{d \over {2r}}} \right)^2 } } - \frac {1} {\sqrt {1 + {\textstyle{{dy} \over {r^2 }}} + \left( {\textstyle{d \over {2r}} } \right)^2 } } \right] \\& = \frac {q} {4\pi \varepsilon _0 r} \frac {3d^2 } {2r^4 } \left( x^2 - y^2 \right)$

だとされていますが，この式変形が良くわかりません．自分で計算すると，

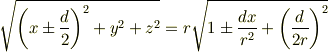
$\sqrt {\left( x \pm \frac {d} {2} \right)^2 + y^2 + z^2 } = r\sqrt {1 \pm \frac {dx} {r^2 } + \left( {\frac{d}{2r}} \right)^2 }$

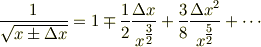
$\frac {1} {\sqrt {x \pm \Delta x} } = 1 \mp \frac{1}{2} \frac {\Delta x} {x^{ \textstyle {3 \over 2} } } + \frac {3}{8} \frac {\Delta x^2 } {x^{\textstyle{5 \over 2}} } + \cdots$

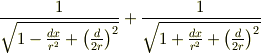
$\frac {1} {\sqrt {1 - {\textstyle {{dx} \over {r^2 }} } + \left( \textstyle {d \over {2r}} \right)^2 } } + \frac {1} {\sqrt {1 + {\textstyle {{dx} \over {r^2 }}} + \left( \textstyle{d \over {2r}} \right)^2 } }$

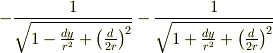
$- \frac {1} {\sqrt {1 - {\textstyle {{dy} \over {r^2 }} } + \left( \textstyle{d \over {2r}} \right)^2 } } - \frac {1} {\sqrt {1 + {\textstyle{{dy} \over {r^2 }}} + \left( \textstyle{d \over {2r}} \right)^2 } }$

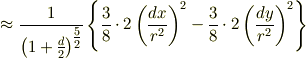
$\approx \frac{1}{{\left( {1 + {\textstyle{d \over 2}}} \right)^{{\textstyle{5 \over 2}}} }}\left\{ {\frac{3}{8} \cdot 2\left( {\frac{{dx}}{{r^2 }}} \right)^2 - \frac{3}{8} \cdot 2\left( {\frac{{dy}}{{r^2 }}} \right)^2 } \right\}$

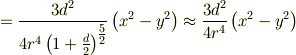
$= \frac{{3d^2 }}{{4r^4 \left( {1 + {\textstyle{d \over 2}}} \right)^{{\textstyle{5 \over 2}}} }}\left( {x^2 - y^2 } \right) \approx \frac{{3d^2 }}{{4r^4 }}\left( {x^2 - y^2 } \right)$

となり，係数が 3/2 ではなく 3/4 になってしまいます．どうかご教示お願いします．

Re: 電気四重極子ポテンシャル

mNeji さんのレス (2008/05/12(Mon) 13:45)

ぱっと拝見して，

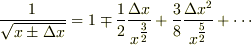
＞ $\frac {1} {\sqrt {x \pm \Delta x} } = 1 \mp \frac{1}{2} \frac {\Delta x} {x^{ \textstyle {3 \over 2} } } + \frac {3}{8} \frac {\Delta x^2 } {x^{\textstyle{5 \over 2}} } + \cdots$

で，変数が微妙に食い違って来ている様なきがします．感触では，

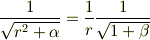
$\frac{1}{\sqrt{r^2 +\alpha}} = \frac{1}{r}\frac{1}{\sqrt{1+\beta}}$

ただし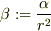， $\beta := \frac{\alpha}{r^2}$ とした．右辺を展開して，

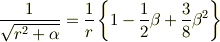
$\frac{1}{\sqrt{r^2 +\alpha}} = \frac{1}{r}\left\{ 1-\frac{1}{2}\beta +\frac{3}{8} \beta^2 \right\}$

として検算されたら如何でしょうか？

Re: 電気四重極子ポテンシャル

yama さんのレス (2008/05/12(Mon) 18:14)

その電荷配置では，対角線の長さが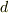の正方形の各頂点に電荷があるわけですね．その場合は，係数は3/4になると思います．

これに対して，１辺が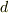の正方形の各頂点に電荷がある場合は係数は3/2になると思います．

もしかすると電荷の配置の解釈が間違っているのではないでしょうか．

Re: 電気四重極子ポテンシャル

のぼりんさんのレス (2008/05/12(Mon) 22:56)

こんばんは．皆さん，回答ありがとうございます．

mNeji さん．

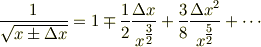
$\frac {1} {\sqrt {x \pm \Delta x} } = 1 \mp \frac{1}{2} \frac {\Delta x} {x^{ \textstyle {3 \over 2} } } + \frac {3}{8} \frac {\Delta x^2 } {x^{\textstyle{5 \over 2}} } + \cdots$

の x は，座標系の意味でなく一般的な変数の積りで書きました．従って，ご説明いただいた趣旨と等価ではないかと思います．

yama さん，実は私も，拙解釈が違っている可能性を最も懸念しておました．質問にも記載したとおり，電荷の配置等に関し，厳密な説明がなかったため，自己流で，記載のとおり解釈していたに過ぎません．ただ，

の部分は，参考書の記述そのものです．この一，二行目からは，先の解釈しか実際にはあり得ないと思うのですが，いかがでしょうか．例えば，各電荷を ±q/2 とし，対角線の長さを 2d と解することはできますが，一，二行目から三行目は導けない様に思うのです．これは，単に本の誤記に過ぎないのでしょうか，それとも何か物理的な意味があるのでしょうか．

Re: 電気四重極子ポテンシャル

yama さんのレス (2008/05/12(Mon) 23:14)

最初の式を前提にすれば，のぼりんさんの解釈で正しいように思います．また，のぼりんさんの計算も合っていると思います．（ただし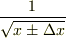， $\frac{1}{\sqrt{x\pm\Delta x}}$ の展開式の第１項は１ではなく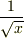， $\frac{1}{\sqrt x}$ だと思いますが．）

参考書の誤記ではないでしょうか．

Re: 電気四重極子ポテンシャル

のぼりんさんのレス (2008/05/12(Mon) 23:21)

yama さん，早々の再回答，どうもありがとうございました．ちょっと安心しました．

数学については多少自信があるのですが，なにしろ物理はからっきし素人なもので，一見，数学的には式変形が誤っている様に見えても，背後に何か物理的な意味があるのではないか，と疑心暗鬼になってしまっています．

皆様，今後ともよろしくお願いします．

[home] [掲示板] [ページの先頭]