δ関数を含む畳み込み
δ関数を含む畳み込み
ゆうや さんの書込 (2008/05/10(Sat) 20:01)
こんばんは. ディジタル信号関係なのですが,わからない問題があるので質問させてください.
問. 信号x(t)=sin2πt(0≦t≦1)が与えられているとき, x(t)とδ(t)+2δ(t-1)-3δ(t-2)との畳み込み積分によって得られる信号の概形を図示せよ.
私の場合,畳み込み積分たδ関数に関する知識も不十分だと思います. この問題にあたりそこから勉強はしたのですが,どうしても分りません.
まず,x(t)*{δ(t)+2δ(t-1)-3δ(t-2)}はどうすればいいのでしょうか. 公式に当てはめようにもよく分からず・・ ∫(-∞→∞)x(τ){δ(t-τ)+2δ(t-1-τ)-3δ(t-2-τ)}dτ =∫(-∞→∞)x(τ)δ(t-τ)dτ+∫(-∞→∞)x(τ){2δ(t-1-τ)}dτ+∫(-∞→∞)x(τ){3δ(t-2-τ)}dτ =x(t)+2x(t-1)+3(t-2)??? これの概形???
と,手の施しようがない感じです. こんなど素人に教えるのは大変だとは思うのですが, 本当に困っているので,どなたか助けてください.
よろしくお願いします.
Re: δ関数を含む畳み込み
mNeji さんのレス (2008/05/12(Mon) 14:07)
遅すぎたかもしれませんが,
>=x(t)+2x(t-1)+3(t-2)???
に,「信号x(t)=sin2πt」を代入して,三角関数の差を積に置き換えるのでは如何でしょうか.ただし「(0≦t≦1)」の条件をどう捉えるか疑問ですが....
Re: δ関数を含む畳み込み
ゆうや さんのレス (2008/05/12(Mon) 22:58)
ごめんなさい. もう少し詳しく教えていただけませんか・・? x(t)+2x(t-1)+3x(t-2)にx(t)=sin(2πt)を当てはめると sin(2πt)+2sin{2π(t-1)}+3sin{2π(t-2)} これを加法定理で展開していくと0になって,概形と言われても良く分りません;
x(t)の代入からがよく分からないので・・; 申し訳ありませんができればもう少し解説をお願いします.
Re: δ関数を含む畳み込み
ゆうや さんのレス (2008/05/12(Mon) 23:24)
続けてすいません.もう少し考えてみました. =∫(-∞→∞)x(τ)δ(t-τ)dτ+∫(-∞→∞)x(τ){2δ(t-1-τ)}dτ+∫(-∞→∞)x(τ){3δ(t-2-τ)}dτ の式を利用して,横軸τのグラフにおこしてみたのですが, t<-2,t>1のとき出力y(t)=0 -2≦t≦-1のときy(t)=3sin2πt -1≦t≦0のときy(t)=2sin2πt 0≦t≦1のときy(t)=sin2πt になりました. これを横軸tのグラフで信号としてあらわしてみると, -2〜1までのあいだの正弦波になります.(波の高さが3,2,1と変化していく感じです)
でもこれだとtoorisugari no Hiroさんの言うtの範囲とずれがありますよね. どこが違うのでしょうか・・? (根本的に違っているのかもしれませんが;;)
Re: δ関数を含む畳み込み
ゆうや さんのレス (2008/05/12(Mon) 23:55)
何度も何度もスイマセン. toorisugari no Hiroさんの範囲で正しかったです; 自分のミスに気が付きました. それからもう一つ,δ(t)+2δ(t-1)-3δ(t-2)の3の前の符号をいつのまにか+にしていました. ここがマイナスなので, 0≦t≦1のときsin2πtのグラフ,1≦t≦2のとき2sin2πtのグラフ,2≦t≦3のとき-3sin2πtのグラフとなったのですが・・ これで良いのでしょうか・・?
一人で騒いで申し訳ありませんが,ご意見よろしくお願いします.
Re: δ関数を含む畳み込み
toorisugari no Hiro さんのレス (2008/05/13(Tue) 12:53)
> これで良いのでしょうか・・? 「
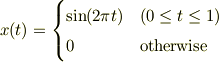
に対して畳み込み 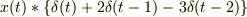 を計算せよ.
」
という問題ならあっていると思います.(個人的には
を計算せよ.
」
という問題ならあっていると思います.(個人的には 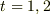 で二重に定義している書き方が気にくわないですが...)
で二重に定義している書き方が気にくわないですが...)
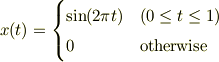
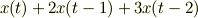
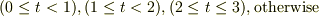 の場合分けです.
の場合分けです.