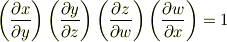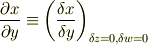偏微分
Re: 偏微分
mNeji さんのレス (2008/05/08(Thu) 08:19)
カラビ=ヤウ空間さん,初めまして.
すこし考えて見たのでコメントします.TeXでの行列などの記法に慣れていないので途中までしか書けませんが....
さて,曲面上の近接した2点,(x,y,z)と(X,Y,Z)=(x,y,z)+(Δx,Δy,Δz)とを考えます.当然,
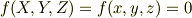
ですが,この関係は関数f(x,y,z)の全微分が高等的にゼロである事を要請しています.
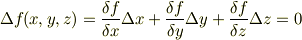
この式を,それぞれの座標の微分で割ってみると3本の式がでます.それを 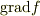 とマトリックスの積に表すと,その積は恒等的に零ヴェクタになります.それが任意の曲面に従う為には,マトリックスの行列式を0と於けば良いように思います.
とマトリックスの積に表すと,その積は恒等的に零ヴェクタになります.それが任意の曲面に従う為には,マトリックスの行列式を0と於けば良いように思います.
ちょこっと計算すると,符号が違うようにも感じますが?
Re: 偏微分
toorisugari no Hiro さんのレス (2008/05/08(Thu) 18:51)
に対して
が成り立つ
は
の関数と考えることができます.そこで
と関数をおくと,恒等式
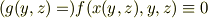
が成り立ちます. 恒等式を微分しても0ですから
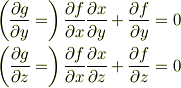
が成り立ち,関係式
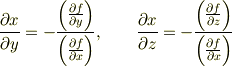
がえられます.
以上の議論を 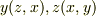 で繰り返せば,その結果を使って
で繰り返せば,その結果を使って
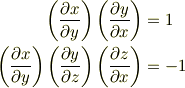
が求まります.
Re: 偏微分
yama さんのレス (2008/05/08(Thu) 21:05)
toorisugari no Hiro さんの証明はきちんとしていてすばらしいと思います.
ところで,直観的で簡便な方法として,次のように考えることもできます.
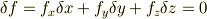
で 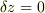 と置くと
と置くと
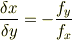
となりますが,左辺の 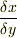 は
は 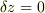 の条件下のものなので,これは
の条件下のものなので,これは 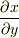 にほかなりません.すなわち
にほかなりません.すなわち
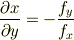
ということになります.
この式で 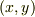 を
を 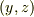 や
や 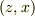 に置き換えれば,同様の式が得られ,それらの3つの式を掛け合わせれば証明すべき式になります.
に置き換えれば,同様の式が得られ,それらの3つの式を掛け合わせれば証明すべき式になります.
Re: 偏微分
カラビ=ヤウ空間 さんのレス (2008/05/08(Thu) 21:06)
mNejiさん,toorisugari no Hiroさん,二人ともありがとうございました.
Re: 偏微分
toorisugari no Hiro さんのレス (2008/05/09(Fri) 17:40)
yamaさん
> 左辺の 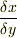 は
は 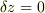 の条件下のものなので,これは
の条件下のものなので,これは 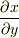 にほかなりません.
にほかなりません.
さらっと書かれたこの解釈,「目から鱗」でした.
自分で書いておきながら 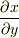 の
の 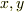 が独立変数になったり従属変数になったりするのが気持ち悪かったのですが,上の解釈は自然ですね.
が独立変数になったり従属変数になったりするのが気持ち悪かったのですが,上の解釈は自然ですね.
勉強になりました.
Re: 偏微分
mNeji さんのレス (2008/05/09(Fri) 21:22)
素朴な疑問ですが,f(w,x,y,z)=0の場合には拡張できるのでしょうかね?
Re: 偏微分
mNeji さんのレス (2008/05/09(Fri) 22:14)
>ここで
> 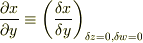 >です.
>です.
なるほど.空間の次数によってパリティが変化して行くというのは面白いです.
すると,この量は空間のもつ絶対的な性質を反映しているのでしょうか?
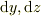 に対して成り立ちます.
に対して成り立ちます.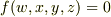 のときも同じにできると思います.
のときも同じにできると思います.