電磁気について
電磁気について
Dai さんの書込 (2008/05/06(Tue) 19:06)
電磁気の基本事項について質問があります. (1)電位の定義
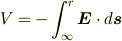
についてですが,マイナス符号がついている理由がいまいちわかりません. 右向きの電界Eの中に単位電荷があると,単位電荷には右向きにEの力が働きますよね.ということはその電荷をEに逆らって左向きに動かすには左向きの力F>Eが必要ではないでしょうか?Fは左向きで電荷が動く方向も左向きだからマイナス符号はいらないのでは?
(2)電気力線についてなのですが,電気力線の接線が電界の向きで,密度が電界の強さとなるのはそれが電気力線の定義だからですか?
(3)電気力線は向きはないのですか?
(4)ガウスの定理
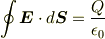
は閉曲面Sを通り抜ける電気力線を数えていると思うのですが,左辺はどうして内積なのでしょうか?閉曲面を垂直に通り抜けるかどうかが電気力線の本数に関係があるのですか?
(5)真空の誘電率の正しい値っていくらですか?透磁率は 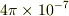 だと思うのですが.
だと思うのですが.
Re: 電磁気について
yama さんのレス (2008/05/06(Tue) 20:40)
(1)変位 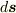 はベクトルであって向きも含んでいます.
右向きを正とすれば,左向きに動くときは
はベクトルであって向きも含んでいます.
右向きを正とすれば,左向きに動くときは 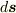 の成分が負になるわけであって,変位が
の成分が負になるわけであって,変位が 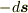 になるわけではありません.
電場から単位電荷にはたらく力は
になるわけではありません.
電場から単位電荷にはたらく力は 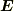 なので,それに逆らって単位電荷を動かすには
なので,それに逆らって単位電荷を動かすには 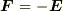 の力が必要となり,その力のする仕事は
の力が必要となり,その力のする仕事は 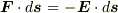 になるわけです.
になるわけです.
(2)定義と考えてよいと思います.
(3)電場の向きが電気力線の向きです.
(4)εE(またはE)が電気力線の密度であって,電気力線に垂直な単位面積あたりの電気力線の本数だからです.
- 光速を
 とすると,
とすると, 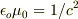 の関係があるので,これから真空の誘電率が求められると思います.
の関係があるので,これから真空の誘電率が求められると思います.
Re: 電磁気について
mNeji さんのレス (2008/05/06(Tue) 21:04)
Daiさんのご質問は多いので,(1)から考えて見ます.
力学的ポテンシャルでは,ポテンシャルの高い所から低い所へ向かって力の場が発生しますね.
電気回路で,電気的ポテンシャルの高い所から低い所に電流が流れます.
この類推から言えば,静電ポテンシャルの高いところから低い所に向かって電場が発生したい訳です.いまある点P, 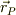 が局所的に極大点だとします.その場合,その近傍点Q,
が局所的に極大点だとします.その場合,その近傍点Q, 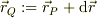 とすると,
とすると,
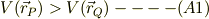
いま, 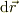 微小変位であることを念頭に,式(A1)の右辺に静電ポテンシャルの式(1)を適用します;
微小変位であることを念頭に,式(A1)の右辺に静電ポテンシャルの式(1)を適用します;
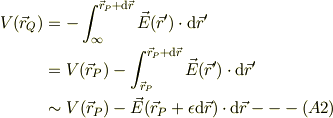
最後の式では,中間値の定理を考慮して,適当な正の微小数  を用いた.
を用いた.
従って,点Pがローカル・マキシマムである場合,式(A1)が成り立つので,
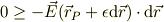
符号を替えると,
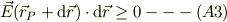
ですね.点Pから任意の方向の微小変位ヴェクタ 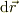 とその近くの電場の方向は同一方向を向いている事になります.言い換えれば,式(1)で定義されたポテンシャルがローカル・マキシマムを持つ時に,その近傍の電場は外にむかって出て行く事になります.
とその近くの電場の方向は同一方向を向いている事になります.言い換えれば,式(1)で定義されたポテンシャルがローカル・マキシマムを持つ時に,その近傍の電場は外にむかって出て行く事になります.
これはわざわざ,回りくどい説明をしました.むしろ等電位面を考えた論議の方が素直でしょうね.以前の質問に書いた様な気がしますが,忘れてしまいました.
Re: 電磁気について
Dai さんのレス (2008/05/07(Wed) 02:29)
お返事ありがとうございます. (1)単位電荷を動かすにはF=-Eの力が必要というところがいままで気になっていました.Fは実際にEと反対方向に働いているのですよね?-Eというと実際には反対方向に働いているような気がしてしまうのですが.
(3)電気力線はベクトルですか?
(5)誘電率は透磁率と光速から導かれるのですか?誘電率と透磁率は独立に決まっているものではないのでしょうか?
Re: 電磁気について
mNeji さんのレス (2008/05/07(Wed) 09:05)
>(1)単位電荷を動かすにはF=-Eの力が必要
ある電荷  が電場
が電場  から作用される力
から作用される力 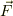 は;
は;
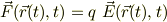
で与えられるので,単位電荷の場合は, 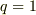 として考えるのでしょう.
として考えるのでしょう.
>(5)誘電率は透磁率と光速から導かれる
「電磁場=電場と磁場」まで進むと,有名なマクスウェル方程式がでてきて,真空中の電磁場の方程式が「波動を表す」ことになります.そこには誘電率は透磁率の積が存在し,波動の伝搬速度との対応が得られます.従って「電磁場の伝搬速度」が「光速」に等しければ,お説の通りだと思います.
Re: 電磁気について
yama さんのレス (2008/05/07(Wed) 10:20)
(1)-EだからEと反対向きになるのですが・・・. なお,単位電荷を動かす向きは必ずしも電場と反対向きではありません.電場の向きに動かす場合や電場に垂直に動かす場合などいろいろな場合が考えられます.従って一般には「電場からの力に逆らって動かす」というよりは「電場からの力とつり合う力を加えながら動かす」としたほうがいいかもしれません. つまり電位とは「電場からの力とつり合う力を加えながら単位電荷を基準点(たとえば無限遠)から考える点まで動かすときに加える力のする仕事」と定義するわけです.この場合は当然Daiさんが書かれた式が成り立ちます. 別の定義として「単位電荷を考える点から基準点(たとえば無限遠)まで動かすときに電場のする仕事」を電位とすることもできます.この場合は
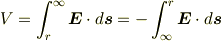
となり,当然ですが同じ式になります.
(3)電気力線はベクトルではなく,向きを持つ曲線です.
(5)マクスウェル方程式によると電磁波の速さが 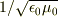 になるので,誘電率と透磁率が独立に決まっていると考えるとこの関係から電磁波の速さが求められることになります.実際,実験的に測定された誘電率の値を用いて電磁波の速さを計算したところ,実験的に測定された光速と等しくなることがわかり,このことから光の電磁波説が提唱されたわけです.
光が電磁波であるとすると,誘電率と透磁率が独立に決まっていると考えても透磁率と光速から誘電率が決まると考えても,マクスウェル方程式が成り立つ限りどちらでも同じことです.ただしその場合,測定に用いる長さの単位が誘電率や光速と無関係に(たとえばメートル原器によって)決められている必要があります.
になるので,誘電率と透磁率が独立に決まっていると考えるとこの関係から電磁波の速さが求められることになります.実際,実験的に測定された誘電率の値を用いて電磁波の速さを計算したところ,実験的に測定された光速と等しくなることがわかり,このことから光の電磁波説が提唱されたわけです.
光が電磁波であるとすると,誘電率と透磁率が独立に決まっていると考えても透磁率と光速から誘電率が決まると考えても,マクスウェル方程式が成り立つ限りどちらでも同じことです.ただしその場合,測定に用いる長さの単位が誘電率や光速と無関係に(たとえばメートル原器によって)決められている必要があります.
しかし現在では長さの単位(m)は光速を基準として定義されています.つまり光速は測定されるものではなく,長さ(と時間)の単位の定義によって決まっているわけです.従って誘電率は,どちらも定義値である光速と透磁率から計算されることになります.
Re: 電磁気について
Dai さんのレス (2008/05/07(Wed) 19:33)
ありがとうございます.
最後に確認ですが,「電場からの力とつり合う力を加えながら単位電荷を基準点(たとえば無限遠)から考える点まで動かすときに加える力のする仕事」の「電場からの力とつりあう力」FはF=-Eで,Eと逆向きに働く力ですよね(ベクトルだと)?
Re: 電磁気について
mNeji さんのレス (2008/05/07(Wed) 20:50)
>最後に確認ですが,「電場からの力とつり合う力を加えながら単位電荷を基準点(たとえば無限遠)から考える点まで動かすときに加える力のする仕事」の「電場からの力とつりあう力」FはF=-Eで,Eと逆向きに働く力ですよね(ベクトルだと)?
なるほど,この意味では,むしろ,電荷粒子の運動方程式のエネルギ積分から考えた方がイメージし易いと思います.少なくとも「準静的にユックリ動かす」という思考の離れ業はいらないのでは?
もう一度おさらいすると,

辺々に 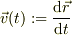 との内積を取ると,
との内積を取ると,
左辺は,
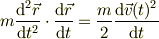
と時間の全微分となります.右辺でも電場が時間に依らず位置だけの関数であれば,辺々に 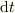 を掛けて時間の積分を考えると,
を掛けて時間の積分を考えると,
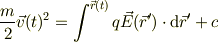
初期条件:時刻 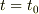 のとき,位置
のとき,位置 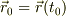 ,速度
,速度 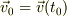 ;とすると積分常数cは
;とすると積分常数cは
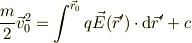
となるので,整理して書けば;
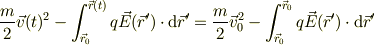
となる.右辺は初期条件のみで決まる量で,それが任意の位置での量と等しいので,辺々は運動によって保存される,全エネルギの保存ですね.初項は運動エネルギ,第二項は静電ポテンシャル;
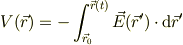
といった流れで感じておけば如何?
数学的にはボロボロでしょうが,静的ポテンシャルを考える時には,「微妙なバランスの元に,無限大の時間を経過して現在に至る」という面倒にはならないと....
Re: 電磁気について
yama さんのレス (2008/05/08(Thu) 00:52)
とつり合う力
は,
なので当然
と逆向きにはたらきます.
ところで,これまでの説明では電位を仕事に関連させて考えたわけですが,直接仕事には関連させず,たとえばmNejiさんのようにエネルギーの積分に関連させて考えることもできますし,または
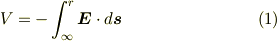
を電位の定義式とすることもできます.ただしこの積分値が積分の終端だけで決まり,途中の経路には関係しないことが必要ですが,静電場の場合は確かにその条件は満たされています.
あるいは次のように考えることもできます. 静電場では

が成り立ちますが,その場合は

となるようなスカラー  が存在することが数学的に示されるので,この
が存在することが数学的に示されるので,この  を電位と定義します.
を電位と定義します.
 には付加定数の不定性がありますが,たとえば無限遠で0になるように決めると
には付加定数の不定性がありますが,たとえば無限遠で0になるように決めると  は(1)式の積分で表されることが導けます.また,(2)が成り立つことからこの積分値が途中の経路に関係しないことも示せます.
また,
は(1)式の積分で表されることが導けます.また,(2)が成り立つことからこの積分値が途中の経路に関係しないことも示せます.
また, 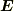 を単位電荷にはたらく力と考えると,(2)からそれが保存力であることが言えるので,それによる位置エネルギーを考えることができますが,それは結局
を単位電荷にはたらく力と考えると,(2)からそれが保存力であることが言えるので,それによる位置エネルギーを考えることができますが,それは結局  であることが分かります.
つまり,電位は単位電荷の位置エネルギーであるということになるわけです.
であることが分かります.
つまり,電位は単位電荷の位置エネルギーであるということになるわけです.