dolphin さんの書込 (2008/05/06(Tue) 05:06)

とてもくだらない質問ですいません． 浮力を積分という言葉を使って説明して頂けませんか？ ちなみに，当方は高校生で，授業で出た課題なので高校生でもわかるようにお願い致します．

yama さんのレス (2008/05/06(Tue) 08:56)

粗っぽくいえば，圧力をその圧力が加わる面全体で積分したものが浮力です． 圧力が加わる面全体というのは，たとえば水中の物体では物体の表面全体，水に浮かんでいる物体では物体表面のうち水面下になっている部分全体です．

もっと詳しく正確な説明は自分で考えてみてください．

mNeji さんのレス (2008/05/06(Tue) 11:23)

dolphinさん，難しい出題をされて大変ですね．私も，高校生の頃は，浮力を一般的に証明できるのかが不思議でした．それ以来，流体は苦手でしたが，今頃になって水泳を力学や流体力学を用いて解析しようとしているので，コメントします(笑)．

当時の疑問を振り返れば；

（１）水圧の高さ依存性：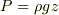

これを示すのに，細長い直方体の「底面にかかる水の重量を底面積で割る」といった感じで導くとおもいました．

（２）ある微小面に働く力：

この説明が当時の高校の教科書では明示されなかったと思います．お持ちの教科書ではどのように書かれていますか？それが判れば，もう少し説明する余地があります．

（３）自分の提案

一般論は面倒なのですが，直方体を考えて，そこに働く垂直成分の力を出してみると良いと思います．いずれにしろ，面積の積分をした結果が，体積の積分に等しくなるのは，とても愉快ですね．大学の授業では，電磁気学や流体力学に沢山の事例が出て来るので，一般論はその時に堪能して下さいね．

なんとなく さんのレス (2008/05/06(Tue) 11:27)

横レス失礼． 高校生ということなので，少しイメージの参考になるものを考えて見ました． 水中の泡（球体とみなす）を考えます．３次元では難しいので，平面で切って，円にしましょう．この円には四方八方から水の圧力が掛かっていますが，それをベクトル（→）で書き込みます．すると，それぞれの矢印は長さが圧力の大きさなので，浮力はその合計になります．円の対称性を考えれば，反対向きの力を打ち消し合った残りの合計がどのようになりますか． このベクトルを細かくしていった極限が即ち，積分です． このイメージで説明を考えれば，どうですか．