きよし さんの書込 (2008/04/22(Tue) 19:23)

直交座標系（ｘ,ｙ）において，ｘ軸とｙ軸ともにθだけ回転して，新しい直交座標系（ｘ’,ｙ’）になるとするときに，

x'＝x*cosθ+y*sinθ y'=−x*sinθ+y*cosθ

になる． というのは，どの参考書を見ても書いてあるのですが，何故そうなるのか，証明的なものがどこにものっていません． 誰か分かる方いらっしゃいますか？

toorisugari no Hiro さんのレス (2008/04/22(Tue) 20:42)

原点からの距離が ，x軸から反時計回りの角度が となる点Pが有ります．xy座標系での点Pの座標は 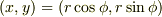となります． x'y'座標系では点Pは原点からの距離が ，x'軸から反時計回りの角度が となる点に見えるので，x'y'座標系での点Pの座標は 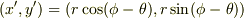となります．

ここまでくれば，後は三角関数の加法定理を使えば終了です．