デバイ長
デバイ長
あやね さんの書込 (2008/04/20(Sun) 21:55)
デバイ長さを求めるために以下の微分方程式の解とその導出方法を探しています.
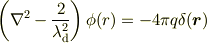
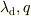 は定数,
は定数,  はデルタ関数であることを表します.
はデルタ関数であることを表します. 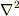 は極座標のラプラシアンです.
は極座標のラプラシアンです.
Re: デバイ長
あやね さんのレス (2008/04/22(Tue) 18:45)
ヒントをありがとうございます.
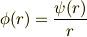
を代入して整理してみました.
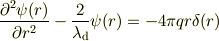
のようになりました.でもこの後がどうしてよいかわかりません.定数変化法を調べてみたのですがよく理解できませんでした.
Re: デバイ長
あやね さんのレス (2008/04/23(Wed) 01:17)
となることから
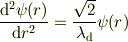
に整理することができました.
この解は  を定数として
を定数として
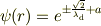
だと思います(二階微分の方程式の解なのに積分定数が一個しかないので何か見落としているような気がします).したがって
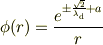
のようになりました.後は境界条件などによって定数の部分を決めるのでしょうか 不完全ではありますがだいぶ答えに近づくことができました.後少しな気がします.
Re: デバイ長
toorisugari no Hiro さんのレス (2008/04/23(Wed) 01:58)
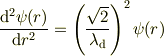
ですね. 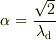 とおくと
とおくと
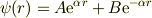
ここで, 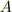 は境界条件
は境界条件 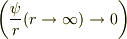 により消えます.
また,
により消えます.
また, 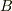 は
は 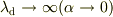 のとき
のとき 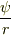 が
が 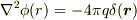 の解
の解  に一致する事から決定できます.
に一致する事から決定できます.
Re: デバイ長
あやね さんのレス (2008/04/23(Wed) 23:14)
いただいたヒントをもとに 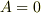 ,
, 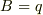 と定数を決定し
と定数を決定し
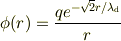
ともとめることができました. これでデバイ長の物理的な解釈とあわせて私なりに理解ができました.丁寧なヒントをありがとうございました.たいへん勉強になりました.
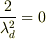 とすればポアッソン方程式ですね.
とすればポアッソン方程式ですね.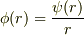 を代入してみては?
を代入してみては?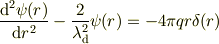
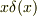 の値は?
の値は?