解析力学の問題
解析力学の問題
夏泉 さんの書込 (2008/04/20(Sun) 19:21)
位置エネルギーが?(x)=klxl^nで表される一次元の系において質量ｍの粒子が運動をする場合の振動の周期をエネルギーＥの関数で表せ
という問題です． 運動エネルギーＴ＝(1/2)mx'^2なので ラグラジアンＬ＝(1/2)mv'^2-klxl^n x>0として，ラグランジュ方程式より mx''+knx^(n-1)=0 というところまで計算したのですが この微分方程式が解けません． どうしたら良いか(あるいはこの方法ではダメなのか)教えて下さい．宜しくお願いします．
Re: 解析力学の問題
yama さんのレス (2008/04/20(Sun) 20:40)
エネルギーの積分を利用してみてはいかがでしょうか．
Re: 解析力学の問題
夏泉 さんのレス (2008/04/20(Sun) 20:56)
アドバイス有難うございます． Ｅ＝(1/2)mx'^2+klxl^n (E-klxl^n)^(-1/2)dx=(2/m)^(1/2)dt ∫(E-klxl^n)^(-1/2)dx=T/4√(2/m) (積分区間は0〜xo) T=4(m/2)^(1/2)∫(E-klxl^n)^(-1/2)dxとなりました． この積分はどう解けばよいのでしょうか?
Re: 解析力学の問題
yama さんのレス (2008/04/20(Sun) 23:19)
面倒そうな積分なので，私も計算したことはありませんが，ランダウ=リフシッツの力学によると，積分区間を[0,1]に変える変数変換によって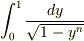 
の定数倍となり，「置き換え 
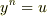によって，積分はいわゆるオイラーの 
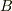積分になり， 
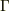関数で表される」そうです．
