一様磁界でローレンツ力による円運動
一様磁界でローレンツ力による円運動
ふぉっくす さんの書込 (2008/04/18(Fri) 01:35)
いつもお世話になっています. ローレンツ力による電荷粒子の円運動についての問題です.
[問題]
一様な磁束密度 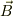 の磁界内で,
の磁界内で, 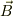 に垂直な速度
に垂直な速度 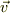 を持つ単位電荷粒子には,
を持つ単位電荷粒子には, 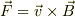 のローレンツ力が働く.
これは常に粒子の進行方向に対して直角の力が働くことを意味する.
したがってその運動は円運動となる.
のローレンツ力が働く.
これは常に粒子の進行方向に対して直角の力が働くことを意味する.
したがってその運動は円運動となる.
ここで,なぜ円運動になるのかを厳密に考えてみましたが,自分の力量では円運動になると完全には言い切れません.
まず,
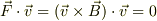 であるから,故に
であるから,故に
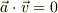
極形式での速度 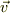 ,加速度
,加速度 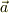 は,
は,
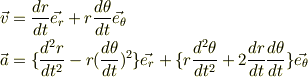
であるからこれを代入して
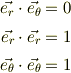
とすると,
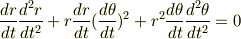
を得る. ここで条件として,
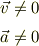
すなわち,
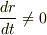 または
または 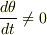 かつ,
かつ,
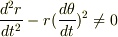 または
または
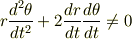
があるから,これを考慮した上で,先ほどの微分方程式を解くと
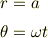
という特殊解が存在する.これは円運動である.
ここまでは計算したのですが,しかし,他にも先ほどの方程式を満たす解が存在しないとも限らないので,円運動以外の運動をする場合もあるかもしれません. また,そもそももっとシンプルに求められるのかもしれません. よろしくお願いします.
Re: 一様磁界でローレンツ力による円運動
toorisugari no Hiro さんのレス (2008/04/18(Fri) 10:29)
かぎしっぽの解説記事
でロドリグの公式の解説があるのでそれを読んでください. それから,つぎのことがいえます. 「微分方程式
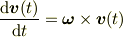
の解は
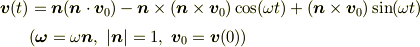
」
これより,
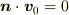 ならば
ならば 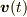 は
は 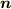 に垂直な面内の円運動になります.点の軌跡も円になることは自明ですね.
に垂直な面内の円運動になります.点の軌跡も円になることは自明ですね.
Re: 一様磁界でローレンツ力による円運動
toorisugari no Hiro さんのレス (2008/04/18(Fri) 13:53)
いきなりロドリグの公式がしんどいなら,
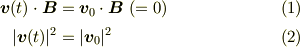
を微分方程式とベクトル積の性質から導けば,題意の  の終点は
の終点は 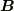 に垂直な面内の円運動をすることは出ますね.あと,「等速」円運動
に垂直な面内の円運動をすることは出ますね.あと,「等速」円運動 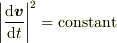 になることを示せば終わりです.
になることを示せば終わりです.
# 「常に粒子の進行方向に対して直角の力が働く」は(2)を意味しますね.
Re: 一様磁界でローレンツ力による円運動
yama さんのレス (2008/04/19(Sat) 09:06)
横から失礼します. この場合の運動方程式を極座標で書くのは,あまりメリットがないと思います. 円運動になるといっても,原点を中心とする円運動とは限らないからです. 原点以外の点を中心とする円運動を極座標で表しても簡単な式にはなりません. 円運動になることを示すにはtoorisugari no Hiro さんのように考えてもいいのですが,デカルト座標を用いて運動方程式を解くのが簡単です.
Re: 一様磁界でローレンツ力による円運動
ふぉっくす さんのレス (2008/04/19(Sat) 17:22)
toorisugari no Hiroさん
大変恐縮なのですが,2つ目の解法について詳しい説明をお願いできますか? 分からない点を挙げたら,結局全部になってしまいました...
・(1)(2)を微分方程式 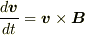 からどうやって求めるのか?
・(1)(2)からどうして円運動と言えるのか?
・等速であることを言うのなら,(2)で十分なのでは?
・そもそも
からどうやって求めるのか?
・(1)(2)からどうして円運動と言えるのか?
・等速であることを言うのなら,(2)で十分なのでは?
・そもそも  は速度ベクトルではない??
は速度ベクトルではない??
Re: 一様磁界でローレンツ力による円運動
toorisugari no Hiro さんのレス (2008/04/19(Sat) 20:39)
えっと,速度ベクトルの方程式だとややこしいので,位置ベクトル  の方程式
の方程式
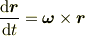
で考えます.この式は以下の関係式を満たします.
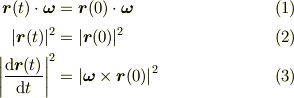
(1)(2)に関しては左辺を微分し,
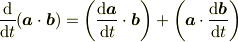
を使い後はベクトル積の性質を使えば導けます.(3)は4重積の計算をして(1)(2)の結果を代入して元に戻せば導けます.
(1)は軌道が 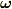 に垂直な平面内にあることを示します.特に初期に
に垂直な平面内にあることを示します.特に初期に  と
と 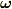 が垂直なら,軌道は,原点を含み
が垂直なら,軌道は,原点を含み 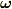 に垂直な平面内にあります.
(2)より
に垂直な平面内にあります.
(2)より  は原点を中心とする球面上に有ることがわかり,(1)により円周上にあることがわかります.
(3)は等速運動を意味します.
は原点を中心とする球面上に有ることがわかり,(1)により円周上にあることがわかります.
(3)は等速運動を意味します.
ただ,これらはベクトルに慣れてなければ難しいでしょうから,yamaさんがおっしゃる方法
「 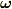 の方向にz軸をとり,
の方向にz軸をとり, 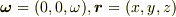 として,
として, 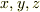 の連立1階常微分方程式を導き,
の連立1階常微分方程式を導き,
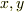 の式から
の式から  を消去し
を消去し  の2階常微分方程式にして,それを解く.」
をされるのがいいと思います.(単振動の微分方程式は解けますよね?)
の2階常微分方程式にして,それを解く.」
をされるのがいいと思います.(単振動の微分方程式は解けますよね?)
なお,どちらの方法でも
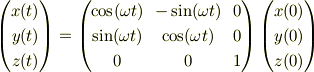
に相当する式が出てきます.ローレンツ力の場合は位置ではなくて速度の関係式になりますが,積分すれば,位置の関係式を得ることは簡単です.
Re: 一様磁界でローレンツ力による円運動
ふぉっくす さんのレス (2008/04/20(Sun) 17:05)
toorisugari no Hiroさん 説明ありがとうございます. ベクトルのほうでちゃんと理解して解けました. 微分方程式の方法はまだこれからですが,たぶん大丈夫だと思います. 皆さん,ありがとうございました.