クーロンの定理とコンデンサの電界
クーロンの定理とコンデンサの電界
ふぉっくす さんの書込 (2008/04/16(Wed) 04:37)
コンデンサの極板間の電界を求める問題で，極板を導体としたときに混乱してしまいました．
まず，極板を単に平面とした場合と，導体とした場合の解き方を示します．
[単なる平面] 極板を，電荷密度±σに帯電した平面（厚さを考えない？）と考えた場合． まず，1枚の極板が作る電界E1を考える． 円柱を考えてガウスの法則を適用することで，電界E1は極板に垂直に， E1・2(底面積) = σ・(底面積)/ε0 E1 = σ/2ε0 となる．極板は±σで2枚あるため，重ね合わせの原理から，求める電界Eは， E = σ/2ε0 + σ/2ε0 = σ/ε0 となる．
[導体] 一方，極板が厚みがあるような導体のときは，導体中に半分埋まった円柱を考える． 導体中は電界が発生しないので，考えるのは導体表面に発生する，面に垂直な電界だけであり，ガウスの法則を適用すると， EdS = σdS/ε0 E = σ/ε0 となる．（クーロンの定理？） 「したがって，極板間の電界はE = σ/ε0となる」
[問題点] ここで分からなくなりました． 導体の表面付近の電界は確かにE = σ/ε0ですが，最初の問題と同様に2枚の極板があるので，極板間の電界は各極板が作る電界をかせね合わせた結果であり，つまり倍のE = 2σ/ε0となりそうなものです． 答えとして間違っているのは分かるのですが，計算としては間違っていないように思えてしまいます． この問題をどう理解すればよいのでしょうか． よろしくお願いします．
Re: クーロンの定理とコンデンサの電界
ミュフ猫 さんのレス (2008/04/16(Wed) 07:57)
電荷密度±σとは面密度ですか？体積密度ですか？ 面密度なら，厚みがある極板の裏表に電荷が等分されるので， 片側の電荷密度は半分になるのでは？
Re: クーロンの定理とコンデンサの電界
yama さんのレス (2008/04/16(Wed) 18:24)
１枚の導体板だけが存在している場合は，その導体板に電荷を与えると，ミュフ猫さんのおっしゃるとおり，電荷は両面に分布します． しかし，コンデンサのように，反対符号の電荷をもった２枚の導体板が近接している場合は，電荷は向かい合う内側の面だけに分布します．
導体板内部の電場が0になるのは，そうなるように電荷が分布するためです． 反対符号の電荷が帯電した２枚の極板が遠く離れているときは，極板の両面にσ/2の面密度で電荷が分布することによって内部の電場が0になっています． ２枚の極板を近づけていくと電荷の分布に偏りが生じてきて，十分接近すると内側の面がσ，外側の面が0になります．そのように電荷分布が変化することによって導体内部の電場が0に保たれるわけです． 注意すべきは，１つの極板に分布する電荷だけでなく，もう一方の極板に分布する電荷も含めて，全体の電荷のつくる電場が導体内部で0になるということです．
ガウスの法則を適用するときに導体内部の電場を0とするのは，もう一方の極板の電荷の影響を間接的に含めて考えていることになります．従って，さらにその上にもう一方の極板による電場を重ね合わせる必要はありません．
それぞれの極板による電場を別々に求めてそれを重ね合わせる場合は次のように考えます．
まず，１枚の極板Aの電荷がつくる電場はAの内部でも外部（極板間の空間）でも 
で，向きは逆です．向きも考えて極板間の電場を ，導体内部の電場を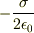 
としておきましょう．
次に，もういっぽうの極板Bの電荷がつくる電場は，極板間の空間で ，極板Aの内部でも になります．
従って，それぞれの極板による電場を重ね合わせると，極板間の空間で 
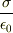，極板Aの内部で0になります．
なお，以上の説明で，それぞれの極板の電荷のつくる導体内部の電場というのは仮想的なものであって，実際に観測される電場は，２つの極板の電場を合成したものであり，これは当然0です．また，導体の誘電率がε0であるということでもありません．
