デッドボールについて

ジュードさんの書込 (2008/04/06(Sun) 12:44)

はじめまして，地方国立大学三年のジュードといいます．化学系ですが，大学レベルの基礎物理学を復習したいと思い，今力学に取り組んでいるところです．質問は，「デッドボールは，当たった後，跳ね返らない方がいたいのはなぜ？」です．初め質量ｍ，速度ｖの物体があり，バッターに当たった時を考えます．

?e(反発係数)≒1のとき

初めpi=mv 終わりpf=mv'(lvl > lv'l) バッターにかかる力 F1=(mv-mv')/t1※ バッターがもらうエネルギー E1= 1/2mv2-1/2mv'2

?e(反発係数)≒0のとき（通常，こちらのほうが危険とされています）

初めpi=mv 終わりpf=0 バッターにかかる力 F2=mv/t2※ バッターがもらうエネルギー E2= 1/2mv2-E'

※t1<t2(非弾性衝突のとき，バッターはうまく身をそらし，速度の変化時間を長く取ったと考えます)

上記のように考えますと，

（@）E1とE2の大小→1/2mv'2とE'の大小に依存（A）F1とF2の大小→tの大小と(-mv')のFに対する影響の大小

となります．一般に言われているe≒0の時が痛いって言うのは，上の@，AをE2,F2を大きくなるように考えて終わりなのでしょうか？他に何か考慮するべきこと（E2,F2が自明に大きいと思えるような事実）があれば教えていただきたいんです．（デットボールの危険性は，EとFで考えてよいのかもよく分かりませんが・・）長々とすいません．このことについて議論などできたらうれしいです．

Re: デッドボールについて

mNeji さんのレス (2008/04/06(Sun) 13:22)

ジュードさん，初めまして．

私は，水泳の推進力を力学的な観点から大雑把に理解しようと試みている老人です．

さて，ボールをグランンドのどこかに固定されている座標系で眺めたとします；

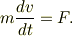
$m\frac{d v}{d t} = F.$

この運動方程式をデッドボールの瞬間の前後の時間のなかで，反発係数を考えて計算するのでしょうか．以下では，ヒトの質量は，ボールのそれに比べて十分に大きく，部分的に動いたりしても全体として，静止しているものと近似します．

反発係数e=1というのは，衝突の前後で「なにも変化がない」，皮膚や筋肉が破壊されたり(出血や組織崩壊がなく)，骨が破壊されずに(簡単な話，骨折しないで)ビールが弾きとばされたという事ですよね．

ですから，左からvで体にぶつかったボールは，左にvで弾き返されるのですから，運動方程式を衝突の前後の短い時間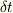， $\delta t$ についての時間積分を考えれば，衝突後の運動量と衝突前の運動量変化について

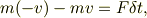
$m(-v)-mv = F\delta t,$

となりませんか．当然，運動の向きだけが変化したので，運動エネルギでの変化はありません．

他方，反発係数e=0というのは，なにか非可逆的な恐ろしい事が起こったのだろうとおもいます．入射したボールが止まる様な事象が発生したのですね．簡単な話としては，どこかに骨折して云々...．

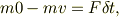
$m0-mv= F\delta t,$

となり，エネルギ変化も最大になる；

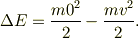
$\Delta E = \frac{m 0^2}{2} -\frac{m v^2}{2}.$

こうして見ると，非弾性衝突の力積が，弾性衝突のそれより大きいのは面白いですね．可逆的にボールをお帰り願う分だけ，力が必要だったという事でしょうね．

Re: デッドボールについて

ジュードさんのレス (2008/04/06(Sun) 17:00)

mNejiさん，さっそくの返信に始めてこの提示版に来たものですごく感激しています．お恥ずかしいことに，e≒1のときの力積は，mNejiさんの言うとおりで，I1（力積）≒2mvですね．ですが，返信の最後の二行の部分の「非弾性衝突のほうが力積が大きい」というのは逆じゃないんでしょうか？すると，非弾性衝突の時の力積は,mvで，?tがあまり変わらないとしたら，単純に力は力積の大きさから，弾性衝突の時のほうが大きい．作用反作用の法則よりバッターにかかる力も弾性衝突の時のほうが大きいことになりませんか？なんどもすいません．m(_ _)m