回転板上を動く虫

回転板上を動く虫

fox さんの書込 (2008/03/22(Sat) 20:44)

剛体の回転とその力学的エネルギーについての問題です．

半径R，厚さd，質量Mの円盤があり，その円周上に大きさの無視できる質量mの虫が静止しており，円板は最初停止していた．円板と虫の摩擦はないものとし，円板の中心軸周りの慣性モーメントをIとする．

(問題) 円板に角速度ω0を与え，一様な回転をさせた．この後，この虫が円周上から中心に向かって歩き出し，そして中心軸からの距離がrになったところで静止した．この結果系の力学的エネルギーは増加したが，その増加量はどれほどか．また，なぜ力学的エネルギーが増えたのか，簡単に述べよ．

出典： http://www.kushiro-ct.ac.jp/ippan/sawa/admission/toko/tkb13.pdf

[考えたこと] まず，虫が移動中も角運動量は保存されると考え，

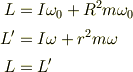
L &= I{\omega}_{0}+R^{2}m{\omega}_{0}\\L' &= I{\omega}+r^{2}m{\omega}\\L &= L'

より，移動中の円板の角速度を

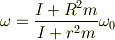
{\omega} = \frac{I+R^{2}m}{I+r^{2}m}{\omega}_{0}

とした．

次に，力学的エネルギーが上がったのは，虫が遠心力に逆らって仕事をしたことで位置エネルギーが高まったからだと考えた．

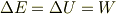
{\Delta}E = {\Delta}U = W

そこで，虫のした仕事を以下のように計算．

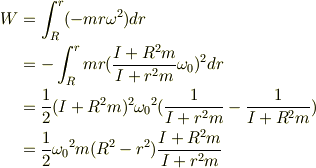
W &= \int_{R}^{r} (-mr{\omega}^2) dr \\&= -\int_{R}^{r} mr ( \frac{I+R^{2}m}{I+r^{2}m}{\omega}_{0} )^2 dr \\&= \frac{1}{2} (I+R^{2}m)^{2} {{\omega}_{0}}^{2} ( \frac{1}{I+r^{2}m} - \frac{1}{I+R^{2}m} )\\&= \frac{1}{2}{{\omega}_{0}}^{2}m(R^2-r^2) \frac{I+R^{2}m}{I+r^{2}m}

[分からないこと] この計算をする前に，円板と虫の運動エネルギーの差を計算したことがあり，円板の運動エネルギー増量は，

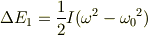
{\Delta} E_{1} = \frac{1}{2}I({\omega}^2 - {{\omega}_{0}}^{2})

虫の運動エネルギー増量は，

{\Delta} E_{2} = \frac{1}{2}Im({\omega}^{2}r^2 - {{\omega}_{0}}^{2}R^2)

となった．両者の和 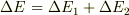\Delta E &= \Delta E_{1} + \Delta E_{2} を計算すると，先ほど求めた虫の仕事Wと同じになった．

そこで良く分からなくなりました． 最初は，虫が仕事Wをして位置エネルギーが高まったので，その分だけ力学的エネルギーが高まったかと思っていました． しかし，先ほどの結果だと，運動エネルギーも，位置エネルギーも，どちらも同じWだけ増えているような気がします． すると，力学的エネルギーの増量は2Wになってしまいますが，虫がした仕事はあくまでWなので，系にそれ以上のエネルギーの増量があるとは思えません． 問題の解き方がどこか間違っているようにも思えます．

このような問題なのですが，よろしくお願いします．

Re: 回転板上を動く虫

ミュフ猫 さんのレス (2008/03/22(Sat) 21:32)

foxさん，こんばんは．

私もよくわからないのですが，「位置エネルギー」とは何のことでしょうか？ 私の浅知恵では，互いの重力（保存力）場による二体間の相対的な共有エネルギー のことを「位置エネルギー」と呼んでいると思ってるのですが． この場合，虫は円板の重心に近づくわけですから，むしろ，位置エネルギーは 減少するような気がします． もし，バネの弾性エネルギーのような意味で，回転座標系の遠心力場による 潜在的な固有エネルギーを「位置エネルギー」と称しているのなら，観測系を 統一すべきではないでしょうか？ 運動エネルギーの算出は，静止系（慣性系）で，「位置エネルギー」の算出は 回転系（非慣性系）では辻褄が合わなくなると思うのですが． ちなみに，円板に対しては「運動エネルギー」という表現も引っ掛かります． 円板の重心は動かないのですから，単に「回転エネルギー」でいいかと．

Re: 回転板上を動く虫

fox さんのレス (2008/03/22(Sat) 23:00)

ミュフ猫さん，ありがとうございます．

ご指摘いただいたことにより，色々あった勘違いやモヤモヤが解消されたような気がします．

位置エネルギーという風に考えたのは，親切な物理という本に 「スケートのスピンで，横に広げた手を真上に広げる場合，手の位置のエネルギーが増える．さらに，回転運動のエネルギーはn倍に増える．後者のエネルギーの増加は，手が遠心力によって開こうとするのに逆らって筋肉がした仕事によって得られる．」 と書かれてあるのを読んで，詳しく読まずに早とちりしてしまったためだと思います． この場合の「手の位置のエネルギー」というのは，単に，手の高さが上がることで，重力によるmghの位置エネルギーが上がるということのようです．

頭の中で整理がついた上でもう一度問題を考えてみると，本の文章にもあるように，虫のした仕事Wの分だけ回転エネルギーが増加したということだと思います． そうなると，2つの方法で出したエネルギーの増加分が等しくなることも，その裏づけとなりそうです．

すっきり解決したような気がします． ありがとうございました．