RLC直列回路について
RLC直列回路について
リコ さんの書込 (2008/03/10(Mon) 17:43)
学校の課題でRLC直列回路の直流電源を接続したときの解が
3つにわかれることと,その振動解がどうなるかを求めよという問題が出たのですが
どうしたらいいかよくわからないので教えてもらえませんか?
ちなみに過渡現象です,よろしくお願いします
Re: RLC直列回路について
tip★ さんのレス (2008/03/10(Mon) 21:09)
では,まず微分方程式を書いてみてください.
Re: RLC直列回路について
トンガリ さんのレス (2008/03/12(Wed) 13:48)
?直流電源Eを接続したときの解?とは回路に流れる電流iを時間tの関数として表すことです. ?解が3つにわかれること?とは?Rのみの回路?RL直列回路?RC直列回路の特徴的な波形に成る事かな・・・
t=0のときi=0として,まずRLC直列回路の電圧平衡式を書いてみると, L(di/dt)+Ri+(1/C)∫idt=Eなる微積分方程式である.私には大学の教科書を持ち出しても式を解けそうもない.
上記の微積分方程式を解くアプローチは?学校の課題?から見て適切でない.解けたとて実用性が乏しいし・・・ オシロスコープを使った実験による体感や,数式的にも別の説明方法があるはずです・・・ 14日(金)納期の仕事が遅れ気味だし,17日(月)確定申告提出期限なので,その後で考えます.
Re: RLC直列回路について
tip★ さんのレス (2008/03/12(Wed) 14:03)
>>?解が3つにわかれること?とは?Rのみの回路?RL直列回路?RC直列回路の特徴的な解に分かれることかな・・・
それは違うと思います.
>>t=0のときi=0として,まずRLC直列回路の電圧平衡式を書いてみると, L(di/dt)+Ri+(1/C)∫idt=Eなる微積分方程式である.私には大学の教科書を持ち出しても式を解けそうもない.
両辺を微分すれば,2階の微分方程式になり簡単に解けます. または,ラプラス変換して解けばモット楽に解けます.(人によって違うかも)
>>上記の微積分方程式を解くアプローチは?学校の課題?から見て適切でない.
微分方程式を解く方法が一番適切とは言いませんが,一般的に電気回路の過渡現象を求めるときは,微分方程式を用いると思います.
>>オシロスコープを使った実験による体感や,数式的にも別の説明方法があるはずです・・・,実用性の問題もあるし・・・
オシロスコープを持っている学生なんてかなり稀です.かといって,学生実験まで待てというのも酷な話だと思います.
Re: RLC直列回路について
トンガリ さんのレス (2008/03/12(Wed) 14:13)
?学校の課題?から見て高校数学程度の知識で理解出来なければと思います. 解けたとて実用性が乏しいし・・・とは大学の教科書による解き方に実用性が乏しいしと言う意味ではなく, 頑張って解いたとて,解の式に実用性が乏しそう・・・と言う意味です.
Re: RLC直列回路について
tip★ さんのレス (2008/03/12(Wed) 15:38)
>>?学校の課題?から見て高校数学程度の知識で理解出来なければと思います.
高校では,コイルは交流のところでしかやってなかったはずなので,RCL直列回路に直流電源を接続するなんて習わないから,大学の方だと思ってアドバイスしてしまいました. ところで,質問者は高校生ですか?それとも大学生ですか?
>>解の式に実用性が乏しそう・・・
どうしてそのように思うのか,理由を聞かせください.
Re: RLC直列回路について
toorisugari no Hiro さんのレス (2008/03/13(Thu) 01:41)
tip★さんがおっしゃるとおり,LCR回路は,いま,高校では扱わないので,大学以上の課題でしょうね.
この式はLCR回路以外にも減衰単振動の式としても有名ですね.
> 解の式に実用性が乏しそう・・・
これから微分方程式,偏微分方程式に進む人には,基本的なスキルとなる問題だとおもいます.
> ?学校の課題?から見て高校数学程度の知識で理解出来なければと思います.
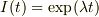 を2階微分方程式に代入すれば,
を2階微分方程式に代入すれば,  の代数方程式(2次方程式)になります.その解を
の代数方程式(2次方程式)になります.その解を 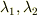 とすれば,
とすれば,
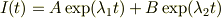
は微分方程式の(一般)解となります( 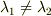 のとき).(この方法,高校でも教わった記憶があります.)
のとき).(この方法,高校でも教わった記憶があります.)
結局,問題の「分類」は2次方程式の解の「分類」に帰着されますね.
Re: RLC直列回路について
rammstein さんのレス (2008/03/13(Thu) 07:47)
解が3つというのは ・過減衰 Over Damping ・臨界減衰 Critical Damping ・減衰振動 Damped Oscillation のことかな...微分方程式をキーワードにして調べてみては.
Re: RLC直列回路について
toorisugari no Hiro さんのレス (2008/03/14(Fri) 13:19)
> 解が3つというのは ... > のことかな...
rammsteinさんがおっしゃるように,
実数値関数 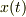 の「実定数係数 線形同次 2階微分方程式」
の「実定数係数 線形同次 2階微分方程式」
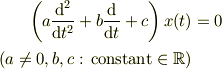
の解は「判別式」 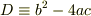 の符号により
・
の符号により
・ 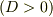 : 過減衰解
: 過減衰解 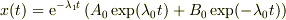 ・
・ 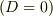 : 臨界減衰解
: 臨界減衰解 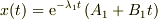 ・
・ 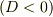 : 減衰振動解
: 減衰振動解 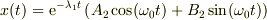 (
( 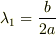 ,
, 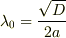 ,
, 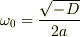 ,
, 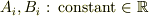 )
に分類されます.
)
に分類されます.
この分類は,微分方程式に 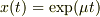 を代入して得られる
を代入して得られる 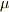 の2次方程式
の2次方程式 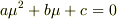 の解を
の解を 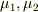 とすれば,
とすれば, 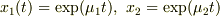 は微分方程式の解であることから理解できます.
は微分方程式の解であることから理解できます.
一般解については,重ね合わせの原理「 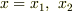 が解なら,
が解なら, 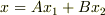 も解」と「
も解」と「 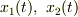 が一次独立な解なら,
が一次独立な解なら, 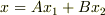 は一般解」から,重解でない場合の,一般解が導出できます.
は一般解」から,重解でない場合の,一般解が導出できます.
重解 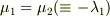 の場合,
の場合, 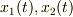 は一次従属(等しい)なので,上記の一般解の構成法は使えません.しかし,
は一次従属(等しい)なので,上記の一般解の構成法は使えません.しかし, 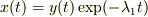 を微分方程式に代入すれば(定数変化法),
を微分方程式に代入すれば(定数変化法),
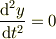
であることから, 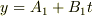 つまり,
つまり, 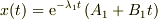 が導けます.
が導けます.