desk さんの書込 (2008/02/20(Wed) 01:56)

高校で学んだ式では解けないので悩んでいます． よろしくお願いします．

列車が直線の線路上を０．２Gの加速度でスピードを上げていて，この列車の中に水槽が固定されています．この水槽の中には水が入っていて，水槽からこぼれることはありませんでした．この水面は，水平に対してどのようになっているかを説明して下さい．その水面の形状を数式で表すことができるのならば，表してください．ただし，Gは，重力加速度を表します．

という問題です． 最初の説明の部分は，重力と加速度があるため見せかけの重量ができ，その見せかけの重力方向と垂直（斜め）になることはわかるのですが，水面の形状を数式で表すことができません．

よろしくお願いします．

トンガリ さんのレス (2008/02/20(Wed) 05:38)

?水面の形状を数式で表すことができるのならば，表してください．?とのことだが， 道路勾配をまねて表すなら，水平100ｍに対して垂直に20メートル上がる坂になる． 道路勾配風20[％］ →ATAN(0.2)の坂→11.31[度]の坂→Y＝−0.2X＋α

toorisugari no Hiro さんのレス (2008/02/20(Wed) 17:44)

> 水面の形状を数式で表すことができません．

問題が不親切です．

(1)水面が定常状態にあるのか，波立ってる状態も考えなければいけないのか書いていない． (2) 「数式」の意味が不明．水面を形成する曲面の式を出せということか，単に傾きを定量的に導出せよなのか，不明．

ともかく「水面は定常状態にあり，そのときは水面は見かけの重力に垂直な平面となる．そのときの水面の(最大)傾きを求めよ．」と考えれば，高校レベルの問題になりますね．

あるいは，平面の式を出したいのなら，以下の考え方を使えばよいでしょう． 「ベクトル 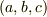に垂直な平面の式は 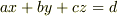( 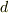は定数)で表せる．」

desk さんのレス (2008/02/21(Thu) 00:00)

トンガリさんご返答ありがとうございます． そのような考え方まったく思いつきませんでした． 参考にさせてもらいます．

toorisugari no Hiroさんご返答ありがとうございます． 確かに自分も解いていて不親切な問題だと感じました． 問題製作者の意図としては高校の知識で解ける問題のはずなので，（２）の場合だと思われます． お手数ですが「水面は定常状態にあり，そのときは水面は見かけの重力に垂直な平面となる．そのときの水面の(最大)傾きを求めよ」という場合の傾きはどのようになるか教えていただけませんか．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/02/21(Thu) 11:07)

ｄｅｓｋさんこんにちわ

「高校の知識で解ける問題のはず」とあります． 加速度運動での問題を慣性力の考え方を使って解くというのは高校では扱っていなかった時期があります．最近復活したということですが多くの高校生は使い分けに戸惑っていると思います． 加速度運動を加速度運動をしている系に乗って見るという立場が徹底できないのです．加速度運動を外から見ていながら解法のテクニックとしてだけ慣性力を使うという便宜的な説明が結構あります．座標系の変換ですから加速度運動を外部の静止座標系から見て運動方程式で解くのと等価なはずです．でも解法のテクニックの立場は慣性力でしか解けないという印象を与えるものです．

この問題と似たものを考えます． 斜面の上に物体を置きます．摩擦はないものとします． 斜面が静止していれば物体は滑り落ちます．でも斜面が加速度ａで運動しているとすると違ってきます．滑り落ちることも滑り上がることも止まることも起こります．斜面の一点に静止したままになるときの加速度はいくらであればいいでしょうか．加速度ａは重力の加速度ｇと斜面の角度θで表すことができます．

加速度座標系慣性力と重力の合力が斜面に垂直 静止座標系重力と垂直抗力の合力Ｆが水平方向を向く． この力が加速度ａの原因の力になる． Ｆ＝ｍａです．

「水面は見かけの重力に垂直になる」ということですから加速度が一定であれば水面の傾きは一定になります．

水面の場合は加速度が決まっていて角度が決まっていない場合です．

某予備校講師 さんのレス (2008/02/22(Fri) 03:55)

komagatakeさんこんにちは．

長年（25年）大学受験の物理に関わってきておりますが，この間，高校物理で慣性力を扱わなくなった時期があったとは記憶にないです．少なくとも大学入試にはあえて慣性力（特に遠心力）を考えてさせて解かせる問題が毎年数問は出ています．確かに加速度系における慣性力の取り扱いには戸惑う高校生も多いのは事実ですが，全て静止系で考えて運動方程式を解くという立場を貫くというのは無理があるような気がします．（少なくともそれでは大学入試には対応できなくなります．もっとも，入試などどうでもいいと言われればそれまでですが．）もちろんご指摘のように慣性力を使わなければ絶対に解けないという印象をもたれる事はそれはそれで問題だとは思います．

例にあげられています加速運動する斜面の問題では，確かに慣性力など考えなくて静止系で見た運動方程式を考えてもいいとは思います．しかし，加速度系での液面の傾き問題では，静止系から見て運動方程式をたてるというのはかえって難しいと思います．液体のどの部分に着目して運動方程式を立てるのか，また各部分（同質量）が受ける力が同じだとしてもなぜ静止液面の傾きが一つに決まるのかは必ずしも自明ではないからです．やはりこの問題では多少感覚的ではありますが「見かけの重力方向」あるいは「見かけの鉛直方向」に液面が垂直になるということを前提として加速度系で考える方がすっきりしていると思います．いかがでしょうか？

トンガリ さんのレス (2008/02/22(Fri) 09:20)

komagatakeさんの斜面の上に物体を置きます．摩擦はないものとします． 加速度座標系慣性力と重力の合力が斜面に垂直 静止座標系 重力と垂直抗力の合力Ｆが水平方向を向く．この力が加速度ａの原因の力になる．Ｆ＝ｍａです．

上記の静止座標系で見た説明に誤りはないが，私には回り道に感じる．何か無理が，欠点が有るのでは・・・ 慣性力は加速度座標系だけで見える『見かけの力』で，静止座標系では使えないと，用語に忠実過ぎるかな・・・

私は慣性力の用語としての歴史に詳しくないが興味がある，私は歴史的常識を無視して， 慣性力とは質量の速度ベクトルが変化させられる時に質量に発生する力と私は解釈します．

これなら，加速度運動を加速度運動をしている系に乗って見るという立場を徹底する必要もなく， 加速度座標系慣性力と重力の合力が斜面に垂直 静止座標系 慣性力と重力の合力が斜面に垂直 で単純で良いと考えます．静止座標系での運動方程は Ｆ＝慣性力 です．

トンガリ さんのレス (2008/02/25(Mon) 14:05)

慣性力の用語としての現在の使われ方に忠実に述べると， ?非慣性座標系に乗って見るという立場を徹底した場合，並進加速度ａも角速度 ω も知り得ない． ?慣性座標系で速度ベクトルの変化を見て，並進加速度ａを知り，向心加速度−Ｒω^2を知る． ?慣性座標系で思案される加速度に質量ｍを掛けて方向を反対にした力−ｍａやｍＲω^2を考えるのは許される． ただし，上記の力−ｍａやｍＲω^2を慣性力と呼んではならない．その理由は用語上の習慣だからである．

私には上記の用語上の習慣がどうしても納得できない． ?慣性座標系で慣性力が禁句で，非慣性座標系で慣性力の使用が許されるのは，日本語として素朴に奇妙である． ?非慣性座標系で『見かけの力としての慣性力』を導入しているが，何だか『慣性力』のネーミングが適切でないと思う． 言葉『慣性座標系での思案に由来する力』が意味不明なまでに短縮されて『慣性力』となったのでは・・・と疑う． ?私は上記?の力こそが日本語として『慣性力』と呼ぶにふさわしい物と思う． 慣性座標系で力の釣り合いとして問題を解ける便利さもあることだし．

権威者であっても，ネーミングが適切でないことは有りうる．言葉は時代と共に変化するものでもあるし・・ 用語の意味は歴史や多数派で決まるもので，私が勝手に変えてみても通用しない．妥協案として， 慣性座標系で『慣性力』の用語の使用を避けるが，力の概念で−ｍａやｍＲω^2の公式の使用は許される． 名無しでは不便なので，?の力−ｍａを『並進慣性抵抗』，ｍＲω^2を『遠心慣性抵抗』と呼ぶことを提案する． 回転座標系での『コリオリの力』に対応しては，慣性座標系では『コリオリの慣性抵抗』と呼ぼう．

慣性座標系で解決できる問題は慣性座標系で考えた方が，曖昧な言葉?みかけの力?を使わなくて明解だ．