直方体に含まれる楕円体の体積

直方体に含まれる楕円体の体積

MAFIA さんの書込 (2008/02/12(Tue) 12:25)

初めまして． 物理の掲示板に計算問題を質問するのは 恐縮ですがよろしくお願いします．

荷電粒子を含んだ電磁場解析には 粒子法(Particle In Cell; PIC)が用いられます．

粒子法では荷電粒子同士に働くクーロン力を直接計算する代わりに 計算格子点の近くに含まれる超粒子から電荷密度を計算し 電位からクーロン力を求めます． これは粒子数の2乗に比例する計算量を低減するためです．

超粒子とは荷電粒子の電荷と質量をまとめた粒子です． 通常の粒子法では超粒子を計算格子と同じ寸法の直方体にします． 計算格子点とは計算格子(直方体)の中心です． 計算格子に含まれる超粒子の体積が その計算格子点に割り当てる電荷量となります．

田中，山本，「計算物理学と計算化学」によると， 直方体の超粒子では偶力が働いてしまうそうです．

これを避けるために超粒子を 計算格子(直方体)に内接する楕円体に変更したいと考えています． すると，求めたい問題は以下のようになります．

辺の長さが 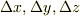\Delta x, \Delta y, \Delta z である直方体に内接する楕円体

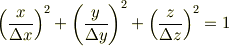
\left ( \frac{x}{\Delta x} \right )^{2} + \left ( \frac{y}{\Delta y} \right )^{2} + \left ( \frac{z}{\Delta z} \right )^{2} = 1

の中心が 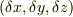(\delta x, \delta y, \delta z) 移動したとき， 直方体に含まれる楕円体の体積は？

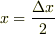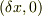これを解くのは難しいので， 第一象限において，直線 x = \frac{\Delta x}{2} と 原点から (\delta x, 0) 移動した楕円

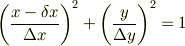
\left ( \frac{x - \delta x}{\Delta x} \right )^{2} + \left ( \frac{y}{\Delta y} \right )^{2} = 1

が囲む面積 S を求めると，

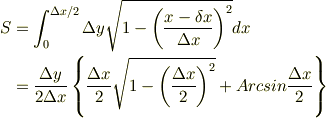
S &= \int_{0}^{\Delta x / 2} \Delta y \sqrt{1 - \left ( \frac{x - \delta x}{\Delta x} \right )^{2}} dx \\&= \frac{\Delta y}{2 \Delta x} \left \{ \frac{\Delta x}{2} \sqrt{1 - \left ( \frac{\Delta x}{2} \right )^{2}} + Arcsin \frac{\Delta x}{2} \right \}

となりました．

ちなみに変数変換 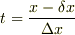t = \frac{x - \delta x}{\Delta x} と 積分の公式

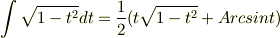
\int \sqrt{1 - t^{2}} dt = \frac{1}{2} ( t \sqrt{1 - t^{2}} + Arcsin t)

を用いました．

この結果を利用して三重積分すれば，上記の問題は解けると思うのですが， 微積分が苦手なので悩んでいます．

長い駄文になりましたが，よろしくお願いします．

Re: 直方体に含まれる楕円体の体積

toorisugari no Hiro さんのレス (2008/02/12(Tue) 19:08)

超粒子あたりにコメントはできません．(何故超粒子が直方体だと偶力が発生して，また，なぜ偶力が発生するとダメなのか興味はあります．また，楕円体だと問題は解決するのかも疑問です．)

ともかく，直方体と楕円体との重なった体積を求める問題としてとらえますね．

ざっと見たところでは，面積の単位(次元)が合っていないように思えます．(Arcsinの引数が無次元量でないのもおかしいです．)計算をもう一度やり直してください． (最初の積分からおかしいような．．．．)

そして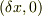， (\delta x, 0) だけでなく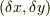， (\delta x, \delta y) も考えれば有る程度見通しはつきますね．

あと，直方体と楕円体で計算するのでなく， スケールし直して単位長さの立方体と球の問題として解けばわかりやすいのでは?

Re: 直方体に含まれる楕円体の体積

MAFIA さんのレス (2008/02/15(Fri) 02:34)

返信が大変遅くなりました． 申し訳ございません．

>>立方体と球の問題として解けば

toorisugari no Hiro様がおっしゃる通り， そのようにすれば簡単に求まるのでは… と思いましたが，うまく積分ができません．

球の断面は円になりますが，欠けた円の断面積をどのように 表現すればよいのでしょうか？

仕方が無いので，

にある「球分」の体積の公式から

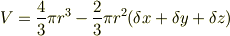
V = \frac{4}{3} \pi r^{3} - \frac{2}{3} \pi r^{2} (\delta x + \delta y + \delta z)

という結論に至ったのですが合っていますか？

Re: 直方体に含まれる楕円体の体積

toorisugari no Hiro さんのレス (2008/02/15(Fri) 03:32)

> うまく積分ができません．

原点と立方体の位置関係で場合分け(かなり大変ですが)して，積分を区分してごりごりやるしかないのでは? 上手なやり方があるのかもしれませんが，初等的解法を力技でがんばってください．

#下の結論はたぶん違うと思います．