FeFe さんの書込 (2008/02/08(Fri) 23:08)

高校生です．赤本の解答を見てどうしても 理解できないところがあったので質問したいと思います． そこには

断熱変化の条件 0=ΔU+PΔV

と，記述してあったのですが，仕事はPΔVではなくて断熱曲線に沿って運動した際の仕事Wにすべきではないでしょうか． 定圧変化→定積変化により断熱曲線上の新しい点に移動したという意味なら仕事はPΔVと表せますが，明らかにPΔV＞Wとなり矛盾します．

いったい何が間違っているのか教えてください．

yama さんのレス (2008/02/09(Sat) 00:41)

初めから断熱曲線というものが決まっていて，その曲線で表される変化が断熱変化であるということではありません． そうではなくて，断熱変化の条件から断熱曲線が決まるのです．従ってまだ決まっていない曲線を断熱変化の条件の中で用いることはできません．

注意しないといけないのは，断熱変化の条件 0=ΔU+PΔV において，ΔUやΔV は無限小変化であるということです．無限小変化の場合はPは一定と見なせるので仕事を-PΔVと表すことができます． もちろん ΔVが無限小でない場合は，Pが一定でないので仕事を-PΔV で表すことはできません． その場合の仕事は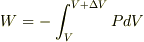， のように積分で表すことができます．

あ さんのレス (2008/02/16(Sat) 00:18)

鋭い質問ですね．仕事はWとしてよいです． また，無限小変化なら-PΔVとできます．

ΔVが無限小変化でない場合は，仕事をこのような積分で表せる保証はありません． 準静過程を除いては，途中の非平衡状態では，熱力学的圧力は定まらないからです．回答した方は，熱力学がわかってない学生さんのようです．

yama さんのレス (2008/02/16(Sat) 10:32)

>準静過程を除いては，途中の非平衡状態では，熱力学的圧力は定まらないからです．

もちろんその通りですが，今問題になっている「断熱変化の条件 0=ΔU+PΔV 」というのは，準静的な場合についての条件です． 従って，ΔVが無限小でない場合は，仕事Wは積分で表すことができます． その場合，断熱変化では 0=ΔU-W が成り立ちます． しかし， 0=ΔU-W が成り立てば断熱変化であるとは言えません． 例えば，系がA→B→Cと変化するとき，A→BではΔU1-W1=Q， B→CではΔU2-W2=-Qであったとすると，A→B→Cの過程全体では 0=ΔU-W が成り立ちますが，Q=0でない限り，A→B→C の変化は断熱変化ではありません． つまり，0=ΔU-Wは断熱変化の必要条件ですが十分条件ではありません． 断熱変化では，単に始状態と終状態の間で0=ΔU-W が成り立つだけでなく，その間の任意の区間で 0=ΔU-W が成り立たなければならず，その場合は結局，任意の無限小区間について0=ΔU-W が成り立つことになるので，0=ΔU+PΔV となるのです．

もちろんWが断熱曲線に沿った仕事であれば，始状態と終状態の間で0=ΔU-W が成り立てば断熱変化です．しかしこれを断熱変化の条件としたのでは循環論法になってしまいます．

追記 別スレに書いたことにも関連しますが，平衡状態の熱力学を適用して非平衡状態の圧力を求めることはできません．しかし圧力の求め方はともかくとして，圧力をPとすれば仕事は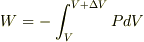， のように積分で表すことができます． これは熱力学に関係なく，力学的に導かれる関係式だからです．これはPが一様でなくて座標の関数となる場合も含みます．