慣性モーメントについて
慣性モーメントについて
リッチ さんの書込 (2008/01/28(Mon) 19:29)
こんばんは．今慣性モーメントについて考えているのですがわからないので教えてください．
まず一つは，円柱です．質量をM，半径をR，慣性モーメントをIとするとI=(MR^2)/2だと思うのですが，これは円板の慣性モーメントを求めるやり方と同じでよいのでしょうか？高さがわからないのでそうするしかないと思うのですが自信がありません．
そしてもう一つは円筒です．薄い円筒はI=MR^2，厚い円筒は内半径をa,外半径をbとするとI=(M(a^2＋b^2))/2となるはずなのですが，導き方がどうしてもわかりません．
何とか理解したいと思いますので宜しくお願いします．
Re: 慣性モーメントについて
toorisugari no Hiro さんのレス (2008/01/29(Tue) 12:13)
円筒の密度を定数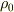 
として，質量 
,慣性モーメント 
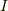は
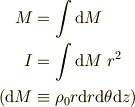
と表せます．あとは積分区間を考えて積分し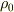， を消去すればいいはずです．
薄い円筒は体積積分でなく面積分をつかうのも手ですが，厚い円筒を上と同様に解いて極限を採ればいいのでは?
Re: 慣性モーメントについて
yama さんのレス (2008/01/29(Tue) 14:14)
まずtoorisugari no Hiroさんが書かれたように，慣性モーメントの定義式に従ってきちんと計算してみてください．
また，次のように考えることもできます．
円柱の慣性モーメントが円板と同じ式で表されることは，積分による定義の式から明らかだと思います．（ただし中心軸まわりの慣性モーメントの場合です．他の慣性主軸まわりについては成り立ちません．）
厚い円筒の慣性モーメントは，半径 
の円柱の慣性モーメントから半径 
の円柱の慣性モーメントを差し引いたものになります．
半径 の円柱の質量を 
とすると，半径 の円柱の質量 
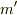は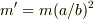 
となるので，円筒の慣性モーメントは
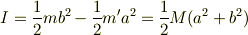
となります．ただし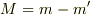 
は円筒の質量です．
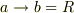とすると薄い円筒になります．
Re: 慣性モーメントについて
トンガリ さんのレス (2008/01/29(Tue) 21:15)
薄い円筒では，半径Rの円周上だけに 質量Mが分布している． 質量Mを円周に沿って多数に分割して 円筒軸周りの慣性モーメントを考え それを全て集めれば， I = MR^2・・・・・・・・・? となるのは明白で，以下に始める計算の積分以前の基礎的大前提である．
Mを使って表す?の式のままでは，厚い円筒の慣性モーメントを 積分するのに不都合なので， 密度ρ，高さH，半径R，厚さ t の 薄い円筒を考えると， 円筒の 断面積 は 2πRt であり， M=2πρHRt・・・・・・・? である． ?を?に代入して， I = 2πρH(R^3)t・・・・? である． （??を使わず，I の定義から?の式を直接立てるも可） 以後?を使わず，?と?を使って計算する．
円筒の厚さ t は薄いので，円筒の半径Rの微小な変化dRに 置き換えて 積分の式を書く． 厚い円筒の 内半径 a から 外半径 b への積分は， ?より ∫2πρHR・dR = πρH(b^2-a^2) だから， M=πρH(b^2-a^2)・・・・・・・・・ ・・・・・? である． (円の面積の公式を使って求めるも可）
?より ∫2πρH(R^3)・dR = πρH(b^4-a^4)/2 = πρH(b^2-a^2)(a^2+b^2)/2 だから， I = πρH(b^2-a^2)(a^2＋b^2)/2・・・・? である． ?を?に代入して， I = M(a^2＋b^2)/2 ・・・・・・・・・・・・・? を得る．
?に a=0,b=R を代入し 円柱の式 I = (MR^2)/2 を得る．（内半径0から外半径Rへの積分で求めるも可） 円柱の慣性モーメントが円板と同じ式で表されるのは，高さがMの中に埋没していることから納得できる．
薄い円筒の?と? 厚い円筒の?と?は 全て公式として使える式であるが， Mを使って表す?や?の式では，ρやHがMの中に埋没しているので，見通しが悪いが・・・ 長所もある． ?の(a^2＋b^2)/2をよく見ると 半径の2乗平均√((a^2＋b^2)/2) の2乗である．?への一般化のために， これを 『相当慣性半径』 の 2乗と 見立てて， √((a^2＋b^2)/2) を 『円筒の相当慣性半径』と通常呼ぶ．
『相当慣性半径』 はρやHに無関係で断面の形状のみに依存する値であるので断面の性質の一つと言える． 機械設計者は強度計算などで断面の性質に習熟させられるので，慣性モーメントへの応用が容易である． 円の面積の公式を使って円筒の体積が求まる様に，断面の基礎的公式を使って『相当慣性半径』が求まる． 複雑な断面形状の場合でも，古い2次元CADを使えば，『相当慣性半径』は自動計算結果の3個の値より √((X軸周りの断面2次モーメント＋Y軸周りの断面2次モーメント)/断面積）で簡単に求まる．
