2重振り子

針さんの書込 (2008/01/21(Mon) 18:00)

はじめまして！学校でわからない課題が出たのでお知恵を拝借したく，書き込んでみました．

早速本題です．２重振り子の解析についてなのですが，ラグランジュの運動方程式を使う方法はいろんななテキストに載っているのでなんとかわかりましたが，ニュートンの運動方程式を使って解く方法が考えても調べても分からなくて困ってます・・・どうやら行列を使うらしい，程度は分かったのですがそれ以上はどうも・・・もし，お分かりになる方がいらっしゃったら是非ご教授お願いします．m(_ _)m

ずっと寒い日が続いていますね．皆さんお体に気をつけて・・・

Re: 2重振り子

yama さんのレス (2008/01/21(Mon) 23:06)

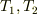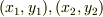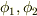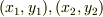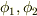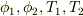それぞれのおもりには，重力と糸の張力がはたらきます．糸の張力を T_1,T_2 ，おもりの座標を (x_1,y_1),(x_2,y_2) として運動方程式をつくります．この運動方程式は４つの式からなります．糸が伸び縮みしないという条件があるので，４個の座標のうち２個だけが独立です．そのため，それぞれの糸が鉛直方向となす角度を $\phi_1,\phi_2$ とすると， (x_1,y_1),(x_2,y_2) を $\phi_1,\phi_2$ によって表すことができます．（これはラグランジアンをつくる場合も同様ですね．）その結果， $\phi_1,\phi_2,T_1,T_2$ を未知数として含む４つの方程式が得られます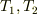． T_1,T_2 を消去すれば，ラグランジアンから導かれる方程式と同じ方程式が得られます．

Re: 2重振り子

針さんのレス (2008/01/22(Tue) 01:54)

まさかこんなに早くお答えがいただけるとは思いませんでした！ありがとうございます！

yamaさんのご指示どうりに計算してみたところ，確かにラグラジアンから出る式と同じ式が出てきました．行列とかを無理に使うよりもずっと考えやすい方法ですね！てっきり行列の対角化とかしたりしないと解けないと思っていたので驚きです・・・おかげさまで私の課題は一段落しました！（本当にありがとうございます！）

ところで，私がずっと考えてもできなかった行列を使う方法（実は先生にヒントとして行列を使うことを教えてもらったのです）というのも好奇心的な意味合いで知りたいのですが，もう一度，おわかりになる方がいらっしゃったら，ヒントだけでもお教えください！今わかってることは ?運動方程式から単振動の方程式に作り直す ?対角化を使うということだけです・・・よろしくお願いします．

Re: 2重振り子

toorisugari no Hiro さんのレス (2008/01/22(Tue) 11:59)

行列で解く方法とは近似解法の一つです．変数の2次以上の項を微小として省いた式が該当します．多項式でない関数はテーラ展開を使って一次式で近似します．(線形化)

例えば単振り子は

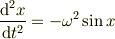
$\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -\omega^2 \sin x$

ですが，一次の近似で単振動

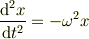
$\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -\omega^2 x$

となりますね． $\phi_1,\phi_2$ を含む式も同様に線形化すれば，連立の線形微分方程式が得られるはずです．それは行列表示と同値です．

Re: 2重振り子

yama さんのレス (2008/01/22(Tue) 15:54)

運動方程式を導くだけなら，行列を用いる必要はありません．運動方程式を近似的に解く場合に行列を利用する方法があるわけです．

運動方程式は連立の非線形方程式なので厳密に解くのは困難です．そこで，toorisugari no Hiroさんが説明されたような線形近似を行って，連立の線形微分方程式にするわけです．この連立方程式を解く方法として，１つの変数（座標）を消去して，1変数だけの方程式にすることが考えられますが，それはなかなか難しそうです．そこで適当な座標変換を行って，それぞれ１つの座標だけを含む２つの単振動の方程式に変換します．この新しい座標を基準座標といいますが，この座標変換を行うために行列の対角化を利用します．このようにして多自由度の系の振動の方程式を解く方法は，大抵の力学の本に説明されているのでよく読んでみてください．

Re: 2重振り子

針さんのレス (2008/01/22(Tue) 22:07)

toorisugari no Hiroさん，yamaさん，ありがとうございます．行列は近似だったのですか・・・微分方程式を解くための道具だったとは・・・

なんだか，一つの問題だったのに凄く多くの事がわかった気がします！自分の知るべきことも分かりました！もう一度力学の本を読んでみます．

お二方とも，貴重なお時間を割いて教えてくださってありがとうございました！これからも度々来ると思います．皆様も，どうぞよろしくお願いします．

[home] [掲示板] [ページの先頭]