慣性モーメント

慣性モーメント

五郎 さんの書込 (2008/01/09(Wed) 21:54)

もうひとつ質問させていただきます．

なぜ薄い直方体の重心のまわりの慣性モーメントの式は

I=(1*M*(a^2+b^2))/12

となるのですか？この式の導き方を教えてください．

Re: 慣性モーメント

toorisugari no Hiro さんのレス (2008/01/09(Wed) 22:21)

辺の長さが 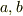a,b の長方形の，板の重心を通り板に垂直な軸まわりの，慣性モーメントの式を求めるには，面密度を \rho とおいて，

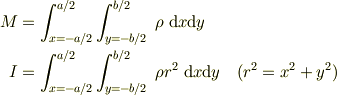
M&=\int_{x=-a/2}^{a/2}\int_{y=-b/2}^{b/2}~ \rho ~\mathrm{d}x\mathrm{d}y\\I&=\int_{x=-a/2}^{a/2}\int_{y=-b/2}^{b/2}~ \rho r^2 ~\mathrm{d}x\mathrm{d}y\quad (r^2 = x^2+y^2)

を計算すれば良い．

Re: 慣性モーメント

なんとなく さんのレス (2008/01/10(Thu) 12:57)

五郎さん，はじめまして，なんとなくです． どのレベルで答えて良いの分かりませんが，toorisugari no Hiroさんのレスで本質は尽きていますので，実際的な計算問題として解くやり方を書きます． まず，直交軸の定理は御存知ですか？直方体の重心まわりと書かれていますが，ここの慣性モーメントはあきらかに直方体に垂直な軸まわりの場合ですね．薄い直方体（長方形の板と思えば）の面内に辺に平行にX軸 ,Y軸をとれば，それらの軸の回りの慣性モーメントをそれぞれIx,Iyとすると，その交点に垂直なZ軸回りの慣性モーメントIzはIz=Ix+Iyとなり，これを直交軸の定理といいます． ところで，Ixは長方形の板をその2等分線を軸として回転する場合ですが，慣性モーメントに関与するのは軸に垂直な長さのみであり，結局，棒と同じ事になるので，辺長をaとすると，Ix=M(a/2)^2/3です．同様に，Iy=M(b/2)^2/3ですから，Izは上記定理より直ちに求まります．