外積とテンソルの内積
外積とテンソルの内積
るっこら さんの書込 (2008/01/08(Tue) 07:35)
ある電磁気学の論文で(Bは磁束密度です)
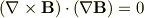
は明らかなので,と述べられておりそこから論旨が展開されています.
Bはベクトル量ですから,外積 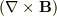 はベクトル.
そしてドットの右側はベクトルのgradをとっていますので3×3のテンソルになると思われます.
はベクトル.
そしてドットの右側はベクトルのgradをとっていますので3×3のテンソルになると思われます.
ここで対象としている磁場は直交座標の1成分しかなく,この場合には成分別に計算するとゼロになるのですが,上記の式は座標系によらずベクトル解析の基本原理を用いていつでも導ける自明の関係なのでしょうか...? 恐らく電磁気の知識(マクスウェル方程式)は全く関係ないかと思います.(この後この原理を用いて電磁気の証明をするので)数学的にご説明のつく方がいらっしゃいましたら教えてください.よろしくお願い致します.
Re: 外積とテンソルの内積
toorisugari no Hiro さんのレス (2008/01/08(Tue) 14:49)
> 上記の式は座標系によらずベクトル解析の基本原理を用いていつでも導ける自明の関係なのでしょうか...?
一般には成り立たないと思います.(軸座標系で 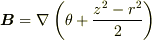 と書ける場合は0にはなりません.)
と書ける場合は0にはなりません.)
> ここで対象としている磁場は直交座標の1成分しかなく
これは 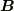 が定ベクトル
が定ベクトル 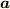 とスカラー場
とスカラー場 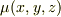 を用いて,
を用いて, 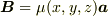 と書ける場合に相当すると思いますが,このとき
と書ける場合に相当すると思いますが,このとき 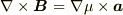 ですから,
ですから,
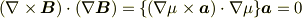
となり,「明らか」といっても良いと思います.
なお, 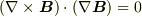 となる
となる 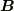 が一般にどのようなクラスに属するかはわかりません.
(2次元的な場
が一般にどのようなクラスに属するかはわかりません.
(2次元的な場
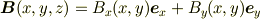
も含まれることはすぐ導けますが...)
Re: 外積とテンソルの内積
るっこら さんのレス (2008/01/09(Wed) 00:01)
迅速のご解答をありがとうございます.
Bはここでは磁束密度であり定ベクトルです.
定ベクトルの場合成り立つことは非常に明快に理解できました.
その他の場合にも,反例を挙げて下さりためになりました.
必ず成り立つわけではないと云うことになったので,該当の論文はあくまで定ベクトルの磁束密度に対して自明である,と述べていたのだろうと納得しました.
一般にどのような 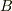 で成り立つかは興味深いところではありますが,今回は分からなくてもよいので今回はこれで終わりにしたいと思います.
どうもありがとうございました.
で成り立つかは興味深いところではありますが,今回は分からなくてもよいので今回はこれで終わりにしたいと思います.
どうもありがとうございました.