ガウスの定理
ガウスの定理
るい さんの書込 (2008/01/06(Sun) 21:46)
わかりません..
ベクトル関数J=(xy,y^2.z)について,ガウスの積分定理の左辺および 右辺を別々に計算し,等価であることを確認せよ. ただし,閉局面Sおよびその中に含まれる領域Vは
S;x^2/a^2+y^2/b^2+z^2/c^2=1
V;x^2/a^2+y^2/b^2+z^2/c^2<=1
で与えられる. 何度も読みましたけどわかりません. 教えてください.
Re: ガウスの定理
tip★ さんのレス (2008/01/07(Mon) 09:59)
閉曲面Sの面積と閉曲面Sの法線ベクトル,領域Vの体積を求めることができたら,この問題は解けそうですね.
簡単のために,まずは,半径rの球でやってみたらどうですか?
Re: ガウスの定理
yama さんのレス (2008/01/08(Tue) 17:09)
面積や体積は計算しなくてもよいと思います.ガウスの定理なので
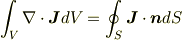
すなわち
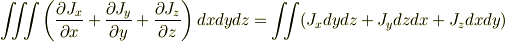
が成り立つことを示せばいいでしょう. 両辺をそれぞれ計算して等しいことを示すのですが,そのためには
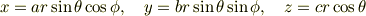
と置いて,変数を 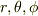 に変換して計算すればいいでしょう.
曲面S上では当然
に変換して計算すればいいでしょう.
曲面S上では当然 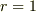 です.
です.