そう（大学２年） さんの書込 (2007/12/26(Wed) 00:49)

始めまして． 現在，大学２年生の「そう」です． 自分の物理レベルは， ↓の，図１くらいの電気システムならなんとか理解できる程度で， 力学は特に苦手です．

Ｒ１Ｒ２ ＿＿＿＿＿＿＿＿ ――｜｜―――――――｜｜――――― ｜――――｜――――｜ ｜｜｜ ＋｜ ｜Ｃ１｜ Ｃ２ ｅ○―― −｜ ―― ｜｜｜ ｜｜｜ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

図１：電気システム

○問題 図１のような電気回路とアナロジーの関係にある機械システムおよび 流体システムを示せ．そして，これらシステムに共通する数学モデルを示せ （Ｃ１，Ｃ２の横断変数をp1,p2として， これを状態変数として状態方程式を作れ）

という問題なのですが，

注：Ｒ１，Ｒ２は抵抗， Ｃ１，Ｃ２はキャパシタ， ｅは電圧を表す．

・分からないところ ：アナロジー関係にある機械システム， 流体システムを求める手順が分からない ・どこまでできたか ：図１の電気システムの状態方程式を求めることはできた ◎出典 ：浅居 喜代治 編著，「基礎 システム工学」，オーム社

教科書を熟読し，インターネットでも調べてみたのですが， アナロジーの見つけ方がよく分からないので， よろしくお願いします．

toorisugari no Hiro さんのレス (2007/12/26(Wed) 13:06)

問題の意図するところはさっぱりわかりません．特に状態方程式は??

とりあえず，正攻法で解くなら，まず微分方程式です．

たぶん，連立1階常微分方程式系を介して2階定数係数同次常微分方程式になるでしょう．パラメータによって減衰解，減衰振動解が得られます．

それと等価なシステムを考えれば良いでしょう．

機械なら減衰単振り子と考えたいところですが，他にあるかもしれません．ふたつのバネと空気抵抗が有るシステムで何か考えられないかな?

流体なら結合振動子かな? 正確な名前は知りません．穴のあいたコップをふたつ用意して水槽に半分だけつけると，それぞれのコップの水量がシンクロして振動するシステムです．それを参考に回路図に近い装置を考えれば?

トンガリ さんのレス (2007/12/26(Wed) 21:46)

図１の電気システムの状態方程式を求めることはできた とのことですが，それで十分結構なことです． この電気回路に相当する機械機構や流体回路 を求めさせるのは教授の邪道だと思います．

30年位前の月刊誌『機械の研究』(養賢堂)では 機械機構や流体回路？の動的性質を解析するのに， それを等価な電気回路に置き換えて考える． の教育的記事の連載があったのを記憶してます．

本題の場合はコンデンサが2個あって問題を複雑にしています． 手始めに，コンデンサが1個の簡単な回路で，あえて この電気回路と等価な機械機構や流体回路を探されたら・・・

電圧と等価なのは機械での力や圧力・・・，それとも速度か知らん． そうだ，モビリティなる概念を使っていた様だ．

そう（大学２年） さんのレス (2007/12/26(Wed) 23:10)

toorisugari no Hiroさん， トンガリさん， 分かりやすい解説， ありがとうございます．

少し方法が分かってきたので，なんとか自分で解いてみようと思います．

トンガリ さんのレス (2007/12/28(Fri) 15:56)

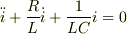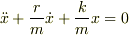(１）回路方程式 と 運動方程式 を見比べると， 電流 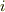に等価なのは位置 でしょうか・・・私には違和感があります．

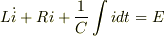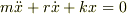(２）回路方程式 と 運動方程式 を見比べると， 電流 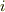に等価なのは速度 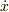でしょうか．この方が私には違和感がありません． この比較では， 抵抗 に等価なのは粘性抵抗 で，違和感がありません． コイル に等価なのは質量 でしょうか ??? 『コイルの電圧は電流の変化に比例する』と『質量に働く力は速度の変化に比例する』 が似通っているので，まあ納得しょう． コンデンサ容量の逆数 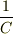に等価なのはバネ定数 でしょうか ??? 『コンデンサの電圧は{電流の積分}÷容量に比例する』と『バネの力はバネ定数ｘ{速度の積分}に比例する』 が似通っているので，これもまあ納得しよう．

二つの微分方程式は似通っているが，直観的に今一つ物足りない． 直観的にする為に，電流 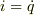電荷の流量を(２)に代入して，

(３）回路方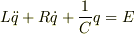程式 運動方程式 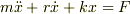って正しいか知らん・・・ご意見をお願いします． 位置 に等価なのは電荷 になるが，本当か知らん・・・ 電圧 に等価なのは外力 になるが，本当か知らん・・・