けん（大学2年） さんの書込 (2007/12/25(Tue) 16:07)

断面積Sのドーナツ状の鉄心（透磁率μ）に導線を一様にN回巻く．このコイルに電流Iを流すとき，鉄心内部につくられるBを求めよ． H，M（磁化ベクトル）も求めよ．

この問題は，ドーナツの軸からの距離をrとし，アンペールの法則を用いることでドーナツの軸のまわりを回転する方向のBについては簡単に求められるのですが，動径方向と軸と平行な方向のBはどうすれば求められるのでしょうか． よろしくお願いします．

yama さんのレス (2007/12/26(Wed) 14:28)

たぶんNは十分大きいと考えてよいのだと思いますが，その場合，コイルの電流を多数の円電流の集まりと見なすことができるので，対称性を考慮すると回転方向以外の磁場の成分は0になると言えるでしょう．

ドーナツの軸を含む１つの平面をとり，この平面上の磁場を考えることにします． この平面をはさんで対称な位置にある２つの円電流を考えると，これらの円電流が平面上につくる磁場の成分は，平面に垂直な成分以外はキャンセルしあって0になります．（なぜか分かりますか？） すなわちこの1組の円電流は，この平面に垂直な磁場をつくるわけです． コイルの電流はこのような円電流の組が多数集まったものなので，結局コイルの電流のつくる磁場はこの平面（ドーナツの軸を含む１つの平面）に垂直であることが分かります．

けん（） さんのレス (2007/12/27(Thu) 16:39)

＞ドーナツの軸を含む１つの平面をとり，この平面上の磁場を考えることにします． この平面をはさんで対称な位置にある２つの円電流を考えると，これらの円電流が平面上につくる磁場の成分は，平面に垂直な成分以外はキャンセルしあって0になります．

けん（大学2年） さんのレス (2007/12/27(Thu) 16:49)

途中でエンターを押したら返信されてしまいました．その時はパスワードも入れていませんでした．すみません…．

＞ドーナツの軸を含む１つの平面をとり，この平面上の磁場を考えることにします． この平面をはさんで対称な位置にある２つの円電流を考えると，これらの円電流が平面上につくる磁場の成分は，平面に垂直な成分以外はキャンセルしあって0になります．

ドーナツを，ドーナツの軸に垂直な面で半分に分けます．一方を上，他方を下と呼ぶことにします． ドーナツの軸を含む平面をとると，ドーナツの上と下はそれぞれさらに半分ずつに分かれます．このとき，ドーナツの「右上」と「左上」の対称な部分による磁場を合成し，「右下」と「左下」の対称な部分による磁場の合成と比べます． ドーナツの軸に垂直な平面上ではキャンセルしましたが，それ以外の部分でもキャンセルしますか？

yama さんのレス (2007/12/27(Thu) 17:12)

それ以外の部分でもドーナツの軸を含む任意の平面上でその平面に垂直でない成分はキャンセルしあいます．

けん（大学2年） さんのレス (2007/12/28(Fri) 16:19)

図をかいて考えていたのですが，いまいちわかりません． 数式でキャンセルを示すことはできるんですか？

yama さんのレス (2007/12/28(Fri) 16:28)

数式で示すこともできるし，数式を用いずに示すこともできます．

けん（大学2年） さんのレス (2007/12/28(Fri) 17:16)

数式での示し方を，概略だけでも教えて頂けませんか？

yama さんのレス (2007/12/28(Fri) 23:40)

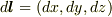ドーナツの軸を含む１つの平面をXY平面にとり，この平面に垂直にZ軸をとります． 点P(x，y，z)を通るコイルの微小部分を とします． XY平面に対してPと対称な点P'(x,y,-z)を通るコイルの微小部分を 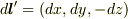とします． また，XY平面上の任意の点をQ(X.Y,0)とし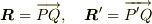， とします． これら２つの微小部分を流れる電流がQにつくる磁場は次のようになります．

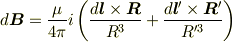
これを計算するとx成分とy成分が0になります．

けん（大学2年） さんのレス (2007/12/30(Sun) 21:35)

どうもありがとうございます．