帯電した導体球殻
帯電した導体球殻
えり さんの書込 (2007/12/23(Sun) 00:06)
度々すみません.違う問題を解いていたのですが,これであっているのか不安だったので書き込みさせていただきました.
内径 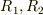 の導体球殻に電荷
の導体球殻に電荷  を与え,球殻の中心に点電荷
を与え,球殻の中心に点電荷  をおいたとき,生じる電場を求めよ.また,点電荷
をおいたとき,生じる電場を求めよ.また,点電荷  の位置が中心からずれると,電場はどうなるか.
の位置が中心からずれると,電場はどうなるか.
という問題で自分なりに考えてみたのですが,球殻の中心からの距離  において
において 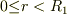 では電場はゼロでよいのですよね?しかし内側の球殻表面上には
では電場はゼロでよいのですよね?しかし内側の球殻表面上には 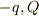 が分布しているので,
が分布しているので, 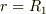 のときは電場は
のときは電場は
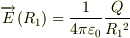 となりますか?(このあたりからかなり自信ないです・・・
となりますか?(このあたりからかなり自信ないです・・・ 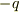 は中心電荷に打ち消されて表面では
は中心電荷に打ち消されて表面では  のみしか影響しないと思いました)
そして
のみしか影響しないと思いました)
そして 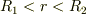 では再び電場ゼロで,
では再び電場ゼロで, 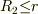 のときは中心電荷の影響で外側の球殻に
のときは中心電荷の影響で外側の球殻に  が分布し,もとからある
が分布し,もとからある  も影響して,電場は
も影響して,電場は
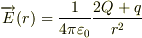 でいいのでしょうか(違うような気がします)..
でいいのでしょうか(違うような気がします)..
考えの間違いを指摘していただけると助かります.どうぞよろしくお願いいたします.
Re: 帯電した導体球殻
tip★ さんのレス (2007/12/23(Sun) 01:32)
で電場が0になるとは思えません.
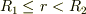 では0になると思います.
では0になると思います.
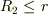 では電荷はQとqだけしかないので・・・
では電荷はQとqだけしかないので・・・
なぜなら,導体の内側の表面には-qの電荷が現れ,導体の外側の表面にはQ+qの電荷が現れるからです.(電荷は保存される)
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 12:14)
では電場はゼロになるのですか・・・?内側の球殻にも
が帯電しているのならば,電場は
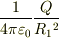 になるような気がするのですが,違うのでしょうか..
になるような気がするのですが,違うのでしょうか..
では,外側の球殻には 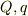 が現れることから
が現れることから
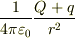 でよいのでしょうか・・・
でよいのでしょうか・・・
さらに初歩的な質問で申し訳ありませんが, 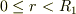 で電場がゼロにならないのは,やはり中心に点電荷があるということだからですよね?これは,導体に囲まれていてもそのようになるということでしょうか・・・?
で電場がゼロにならないのは,やはり中心に点電荷があるということだからですよね?これは,導体に囲まれていてもそのようになるということでしょうか・・・?
Re: 帯電した導体球殻
yama さんのレス (2007/12/23(Sun) 13:09)
この問題については,ガウスの法則
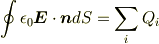
を半径  の球面に適用すればよいと思います.
ただし右辺は球面の内部にある電荷の総和です.
当然ですが
の球面に適用すればよいと思います.
ただし右辺は球面の内部にある電荷の総和です.
当然ですが  の値によって右辺の値は異なります.
の値によって右辺の値は異なります.
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 13:26)
「導体」という言葉に混乱しています.導体球でもガウスの法則は使えるのでしょうか?
Re: 帯電した導体球殻
yama さんのレス (2007/12/23(Sun) 14:18)
導体球というわけではなく,任意の半径  の球面にガウスの法則を適用するということです.
その球面の内部に導体球が含まれていれば,その導体球のもつ電荷も含めて内部の全電荷が右辺になります.
の球面にガウスの法則を適用するということです.
その球面の内部に導体球が含まれていれば,その導体球のもつ電荷も含めて内部の全電荷が右辺になります.
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 14:45)
では,
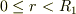 のときは
のときは
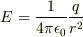
 のときは
のときは
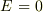
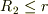 のときは
のときは
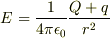 でいいのでしょうか..
でいいのでしょうか..
Re: 帯電した導体球殻
yama さんのレス (2007/12/23(Sun) 15:16)
についてはそれでいいと思いますが,それ以外の部分については違っていると思います.
というのは,問題文からは内径 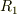 の球殻にも電荷
の球殻にも電荷  が与えられているように読みとれるからです.
が与えられているように読みとれるからです.
あるいは,2つの球殻があるのではなく,内径 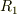 ,外径
,外径 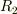 の1つの球殻があるとすればえりさんので合っているとおもいますが・・・.
の1つの球殻があるとすればえりさんので合っているとおもいますが・・・.
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 15:35)
それでは,
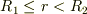 のときは
のときは
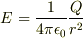
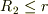 のときは
のときは
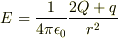 でいいのでしょうか?これだと,導体内部の電場はゼロだということが利いてこないような気がするのですが・・・
でいいのでしょうか?これだと,導体内部の電場はゼロだということが利いてこないような気がするのですが・・・
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 15:42)
>あるいは,2つの球殻があるのではなく,内径 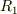 ,外径
,外径 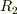 の1つの球殻があるとすればえりさんので合っているとおもいますが・・・.
の1つの球殻があるとすればえりさんので合っているとおもいますが・・・.
この課題は導体がテーマみたいなので,もしかしたら,1つの球殻のことを言っているのかもしれません..ややこしくで申し訳ありません.
もし2つの球殻ならば,No.18957ので合っているのでしょうか?
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 16:28)
上は2つの場合を言っています..
Re: 帯電した導体球殻
tip★ さんのレス (2007/12/23(Sun) 16:29)
内側の球殻の内側の表面には-qの電荷が帯電し,外側の表面にはQ+qの電荷が帯電するんじゃないですか? 電荷は保存されないといけないのでは?
他の人の意見も待ってみましょう!自分の考えも間違っている可能性もあるので.
Re: 帯電した導体球殻
yama さんのレス (2007/12/23(Sun) 17:59)
tip★さんの考え方で合っていると思います.
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 18:38)
すいません,頭がついていっていないので,確認させて下さい. この問題がもし2つの球殻の場合を考えろといっているのであれば, 内側の球殻にも外側の球殻にもそれぞれQが与えられているということですよね?
そしてこの問題では球殻の中心にqの点電荷があるので,内側に-q,外側にqが分布しますよね?
この状態で 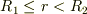 のとき,内側の表面に帯電しているQと-q,さらに中心にあるqが電場に関与して,Q+(-q)+q=Qが半径rの球面内の電荷にならないのでしょうか.
のとき,内側の表面に帯電しているQと-q,さらに中心にあるqが電場に関与して,Q+(-q)+q=Qが半径rの球面内の電荷にならないのでしょうか.
そもそもこの考えで電荷保存がしっかり表せているのかもわからないです. すみません,あと少しお付き合い願います..
Re: 帯電した導体球殻
yama さんのレス (2007/12/23(Sun) 20:34)
中心の点電荷がq,球殻の内側表面の電荷が-q,外側表面の電荷がq+Qなので,合計するとq+Qになります.
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 20:57)
ということは内側にはQは帯電していないということですか?
Re: 帯電した導体球殻
yama さんのレス (2007/12/23(Sun) 22:52)
そうです. もし中心の点電荷がなければ,電荷Qは外側表面に分布します.もし内側表面に分布すれば,導体内の電場が0でなくなります. 中心に点電荷qを置くと,内側表面に電荷-qが生じますが,これは内側表面から電荷qが押し出されるということであり,押し出された電荷が外側表面に移動する結果,外側表面に電荷Q+qが分布することになります.
Re: 帯電した導体球殻
えり さんのレス (2007/12/23(Sun) 23:34)
なるほど.それで導体であることが言えるのですね!! では,外から見たら,あたかも点電荷Q+qがあるように見えるということですね. やっと理解できました.お付き合いいただき,どうもありがとうございました. 大変勉強になりました.
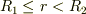 では
では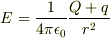
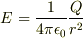 ではないのですか?
(電荷保存で,内側の球殻には-qが分布し,Qしか影響を及ぼさないような気がしました)
ではないのですか?
(電荷保存で,内側の球殻には-qが分布し,Qしか影響を及ぼさないような気がしました)