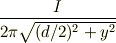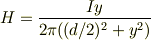電磁気学,磁界についての問題
電磁気学,磁界についての問題
よっしー さんの書込 (2007/12/10(Mon) 22:49)
初めまして. 学部一年生ですが磁界についての復習をしていますが,分からない問題があるので質問させてください.
1)無限直線導体が距離 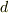 だけ離れて平行におかれている.
この導体に同方向に電流
だけ離れて平行におかれている.
この導体に同方向に電流 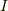 アンペアを流したとき,導体から等距離平面における磁界を求めよ.
アンペアを流したとき,導体から等距離平面における磁界を求めよ.
導体を紙面に垂直に立て,ビオ・サバールの法則を適用して
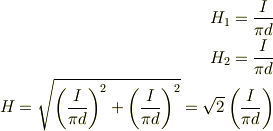
と考えました.合成と考えたのですが愚直すぎでしょうか.
2)半径  の円形導線が同軸上に間隔
の円形導線が同軸上に間隔 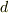 だけ離れておかれている.
それぞれの導体に
だけ離れておかれている.
それぞれの導体に 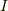 アンペア,
アンペア, 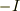 アンペアの電流を流したときの中心軸上の磁界を求めよ.
一つの円形電流が作る中心軸上の磁界は円形に垂直な成分しか残らないから
アンペアの電流を流したときの中心軸上の磁界を求めよ.
一つの円形電流が作る中心軸上の磁界は円形に垂直な成分しか残らないから
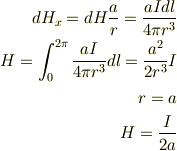
なので,電流が逆向きであれば単純に0と考えたのですが,距離が 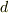 離れているのが気になります.
離れているのが気になります.
間違いなどを指摘していただければ幸いです.よろしくお願いします.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/11(Tue) 00:17)
導線から等距離平面なので答えには変数が入っていないとおかしいと思います. 2問ともそんなに単純な問題ではないと思います.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/11(Tue) 21:44)
1)のみですがもう一度考え直してみました. 1本の無限長電流による磁界の微少量は
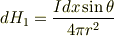
もう一本の無限長電流においては対称性から,題意から
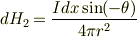
また
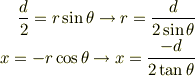
これより
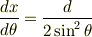
また
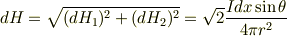
であるから
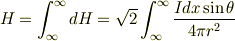
となってしまい結局最初の結果と同様になりました.積分してから足しても足してから積分しても変わらない結果です.方向は
のように考えました.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/13(Thu) 18:38)
よっしーさん,ごめんなさい.
編集したつもりが,削除になって前書いた解説が消えていたようです.
とりあえず,導線を1つだけとして,半径rの閉曲線についてアンペールの法則を適用して,導線が作る磁界を求めてみてください. ビオ・サバールでも良いですが,かなり面倒くさいです.
大きさだけではなく,向きも書いてください.
向きは,電流が流れる方向から  へ右ねじです.
へ右ねじです.
とりあえず,これからやってみてください.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/14(Fri) 07:03)
返信ありがとうございます. 一本の場合ですがNo.18797で導いている方法では間違っているのでしょうか?
ビオ・サバールでは面倒くさいとの事ですが,私はこの方法以外の方法を今のところ下記程度にしか思いつけません.
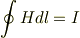
という周積分による.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/14(Fri) 12:02)
では,ビオ・サバールでやってみましょうか.
まず,導線1つについてビオ・サバールの法則を使ってみましょう.そうすると,
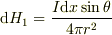
となりますね.ここまでは,よっしーさんが書いてた式と同じです.
この後,よっしーさんは,  をについて解いていますが,
一般的な場所での磁界を今は求めたいと思っているので,
をについて解いていますが,
一般的な場所での磁界を今は求めたいと思っているので,  について
解いていきます.
について
解いていきます.
では,ここで問題です. 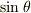 と
と  を求めてください.
ただし,a,x,r以外使用してはいけません.
を求めてください.
ただし,a,x,r以外使用してはいけません.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/15(Sat) 00:12)
違います.
まず図をきちんと描けているか知りたいのですが,
?導線を描く ?導線のどこでもいいので点をとる(そこを点Qとおく) ?導線以外ならどこでもよいので点をとり(その点を点Pとおく),点Qと点Pをつなぐ.これの長さがrです. ?点Pから導線に対して垂直に線をひく.その線と導線の交点を点Oとする.点Pから点Oの長さがaです.
電流は下から上に流れているものとします. また,点Oをx軸の原点として上のほうを+とします. つまり,点Qの座標はxとなります.図の描き方により−xとなったりしますが, +xとなるように点を取ってみてください.
ただし,a,x,r以外使用してはいけません. これをきちんと守ってください.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/15(Sat) 23:42)
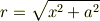
でしょうか. ↑x | |a |---------------------× |/ |/ |/ |/r |/ |θ / ↑/ dx
という風にイメージしています. 身勝手かつご気分を害されるかと思いますが,導線の場合,円形電流の場合は一本だけの場合の私の考えはあっていると思うのですが,そこからの重ね合わせが自信がないです. 一本のみの場合は様々な参考書や教科書に掲載されていますが,重ね合わせの方法が分からないという事は,一本のみの基本も出来ていないという事になるのでしょうか. tips様がよろしければ重ね合わせの部分を重点的に教えていただきたいです.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 00:50)
rはそれであっています.では次,積分の計算をしてみましょう. 積分範囲は−∞から∞です.
円形電流が1つの場合ですが,円の中心という一点の場合の磁界はよっしーさんが書いている式で,あっていますが,中心軸ということに関しては変数が入っていないとおかしいと思います. まずは,1番目の問題から丁寧にやっていきましょう.
>>身勝手かつご気分を害されるかと思いますが,
自分も間違っている可能性があるので,自分が間違っていると思ったところはどんどん指摘してください.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 01:15)
ちょうどいらっしゃったのですね. 失礼な発言にも関わらず対応感謝致します.
![\int^{\infty}_{-\infty}\frac{aI}{4\pi r^3}\\=\int^{\infty}_{-\infty}\frac{aI}{4\pi (a^2+x^2)^{\frac{3}{2}}}dx\\=\left[\frac{axI}{4a^2\pi\sqrt{a^2+x^2}}\right]^{\infty}_{-\infty}\\=\frac{I}{2\pi a}](http://hooktail.maxwell.jp/bbslog/f76214595692a84331843f0472012117.png)
もしくは変数変換でも解けると思います.
ここまで解きましたが今はa=d/2の場合を代入,すれば一本分の電流が作る磁界でしょうか.
ここでちょっと気分を変えて円形電流についても同様に考えてみたのですが, 確かに中心では私の考え通りですが,「軸上」だと,同様な考えで
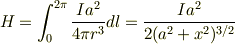
となりますね.ここでx=0であれば中心という事ですから私の最初に示した式ですね・・・.少し先走ってしまいましたがdだけはなれていて電流が逆に流れている場合の円形電流はx軸の取り方が逆になってxがx+dになる,と考えられる・・・のでしょうか.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 01:28)
正解です.
この答えから,磁界はaの関数であるであることがわかります.
ややこしいですが,a→rとしましょう.さっき使ったrと区別しましょう. 導線を中心とする半径rの円を考えると,その円の部分の磁界は一様と考えられます.
次は,磁界の向きを考えましょう.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 01:37)
磁界の向きはちょうどディスプレイを自分側から貫く向きですね.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 01:59)
この直線電流を中心軸とした円筒面,であると思います.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 02:11)
「この問題で」という一つを見落としておりました.申し訳ありません. ちょうどこの導線の中心線をモニタに向かって向こう側にかつモニタに垂直に切った平面ではないでしょうか. ちょうど包丁で切るとモニタが綺麗に半分に割れて中身が見えるような平面と考えています.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 02:37)
等距離平面上で考えて, 縦方向つまりx=d/2軸上では磁界の向きがちょうど反対で大きさが同じなので打ち消し合うので常に0ではないでしょうか.
異なるところ,という意味が理解しづらいです.ちょうど長距離平面の手前〜奥行き方向では何かしらの値を持つ,という事でよろしいのでしょうか.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 02:42)
同じところは,導線と平行な直線を等距離平面にもっていってあげると,その線ではどこでも同じ磁界になります.ですので,x=d/2だけではありません. xが上で使っているのとかぶっているので,区別してください.
異なるところはそれであっています.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 02:47)
上から見た図です.
x←y↑
○・○ P 電流は,紙面の裏から表に流れているものとします.
点Pを原点として,電流が流れる方向を+z,x軸とy軸は図の通りとしてこれから考えていきましょう.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 02:51)
では次です.
さきほど述べたように,zがどんな値であっても磁界はxとyによって決定されるので,簡単のためにxy平面で考えていきましょう.
(0,y)を点Qとします.
左側の導線による点Qの磁界の大きさと向きを述べてください.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 02:54)
文章ではうまく説明しづらく,なおかつこう言うときに限ってスキャナの調子が悪いのでいかんともしがたいと思っていたのですが,調べていたら ttp://www.kagaku.info/faq/ampere991116/index.htm のサイトを発見致しました.
ちょうどこの時のPでの磁界の強さを計算する,というつもりで書いた図がNo.18797の図です. 直接のリンクでは見られないようですが ttp://f40.aaa.livedoor.jp/~itdreams/UPLOAD/gazou.php のNo.1401です.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 03:00)
どこから分からなくなったか,または,説明しづらくなったか,教えてください.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 03:05)
改めて考えればyが先ほどのx,xが先ほどのaという事になりますから 大きさは
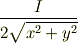
で,方向は左側の導線を中心とした(0,y)を通る左回りの円の接線方向(右ねじから)ではないでしょうか.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 03:10)
向きはあっていますが,大きさが間違っています.
前使ったaとの比較をもうちょっと良く考えてみてください. あとπをぬかないように.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 03:12)
先ほど使ったxというのは,電流が流れ方向がxということにしていたので,これをzとします.
先ほど使ったaというのは,導線から垂直にでた線の長さのことなので,x,y,zのどれにも属しません. なぜなら,その線を回転させれば・・・
さっき,よっしーさんがx=d/2とかいていたので,このxがさっき私が書いた図のxと一致します.ただし,原点の位置が違います.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 03:39)
わかっているようですね.
よっしーさんの図だったら,
→x↓yとしたほうが良いですね.
では,その合成した磁界を求めてください.それで終わりです.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 03:41)
大きさは距離が同じなので等しくなるのは理解できます(d/2が-d/2ですが二乗するので同じという言い方もありますが). 向きは右側の導線を中心とした(0,y)を通る左回りの円の接線方向(右ねじから)ではないでしょうか. つまりこれらを合成すると左向きに磁界が出来るという事になると思いますが,如何でしょうか. ←ー> /
いびつですが正方形の斜辺が合成した磁界でしょうか.
↑電流のつらむく向きが逆のような気がします 解としては
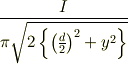
でしょうか. と考えたのですが三平方は使えないのでベクトルの合成をしなくてはならないのですね.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 03:46)
合成したら,右向きの磁界になるはずです. よっしーさんの図もそのようになってますよ.
それと,図には 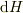 とか書いてありますが,さっき積分しているので,
とか書いてありますが,さっき積分しているので,  でいいですよ.
でいいですよ.
2つの磁界は直交しないことにも注意です. つまり,三平方の定理は使えません.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 04:27)
この場合,合成した結果は綺麗な形にはなりませんが,そういう問題,といってしまえばそれまででしょうか.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 11:44)
まぁ,自分としてはそれほど汚い形とは思いませんが,そういう問題が電磁気学には多いような気がします.
とりあえず,答えを書いてみてください. 上に書いてある式は間違っています.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 15:34)
正解です.
その調子で2番目の問題もがんばってみてください. 2番目の問題は自分もまだ解いていないので,ノーヒントでがんばってください.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/16(Sun) 16:07)
ありがとうございました. やはり二番目は相当に難しいという事でしょうか. ヘルムホルツコイルの電流が逆バージョンという気がしますが,ヘルムホルツコイル自体を講義でやっていないので頑張ってみようと思います.
Re: 電磁気学,磁界についての問題
tip★ さんのレス (2007/12/16(Sun) 16:59)
見た感じだと,1番目の問題とほとんどやり方は同じだと思います.
Re: 電磁気学,磁界についての問題
よっしー さんのレス (2007/12/17(Mon) 21:40)
ほぼ同じやり方で解けました. 磁界の向きが逆と言うことに気をつけて,重ね合わせを行いました. 合成の手順はむしろ1よりも楽でした(何しろ軸上なので). tip様ありがとう御座いました.
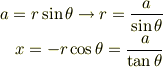
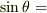 という形にしていただきたかったです.
という形にしていただきたかったです.