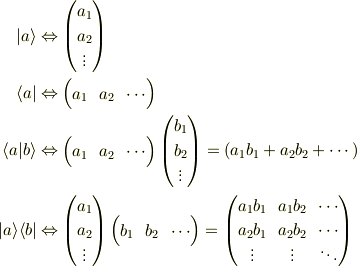ケットブラ?
ケットブラ?
カイ さんの書込 (2007/12/05(Wed) 23:46)
ブラケットはベクトルの内積と同じだから,スカラーになるのはわかるのですが |m><n|みたいになっているのは,どうやって計算するのでしょうか? 縦ベクトル×横ベクトルになると思うのですが.
Re: ケットブラ?
カイ さんのレス (2007/12/06(Thu) 19:29)
ありがとうございます. Σ|j><j|=1っていう公式がありますよね?|j><j|が行列だとすると行列の和,ということになりますが,なぜそれが1(=スカラー)になるのでしょうか?
Re: ケットブラ?
toorisugari no Hiro さんのレス (2007/12/06(Thu) 19:48)
> Σ|j><j|=1っていう公式がありますよね?|j><j|が行列だとすると行列の和,ということになりますが,なぜそれが1(=スカラー)になるのでしょうか?
演算子としての1
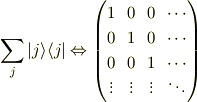
つまり単位行列です.
Re: ケットブラ?
カイ さんのレス (2007/12/07(Fri) 12:00)
返信遅くなり申し訳ありません.何度もすみません. 行列の理解が全然できていなかったので,本を読み直してみたのですが 行列の積の定義は
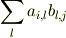
ですよね?今の場合,ケットは1列,ブラは1行なので 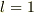 で,ベクトルの成分を具体的に
で,ベクトルの成分を具体的に 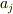 と表示することにすると
ケットブラの行列要素は
と表示することにすると
ケットブラの行列要素は
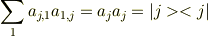
となるように思います. そうすると,
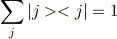
という式のΣの添え字はjではなく1であり,1ならΣはいらないような気がするのですが,どこが間違っているのでしょうか?
Re: ケットブラ?
toorisugari no Hiro さんのレス (2007/12/07(Fri) 12:44)
> ベクトルの成分を具体的に 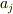 と表示することにすると
と表示することにすると
ここをいい加減にしたらいけません.
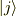 の
の 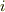 成分は
成分は 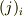 とすべきです.
あるいは,クロネッカーのデルタを使うべきです.
とすべきです.
あるいは,クロネッカーのデルタを使うべきです.
Re: ケットブラ?
カイ さんのレス (2007/12/07(Fri) 14:33)
ブラケットを理解できていませんでした.重大なミスでした. そうすると,
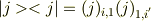
で,もし規格化されていたのならば
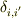 となります.
つまり,単位行列になるということは理解できるのですが,そうするとΣは必要ないのではないのですか?|j><j|だけで単位行列要素を表せてしまっているように思えます.
もし,ベクトルが規格化されていなかった場合,iが一致するところは
となります.
つまり,単位行列になるということは理解できるのですが,そうするとΣは必要ないのではないのですか?|j><j|だけで単位行列要素を表せてしまっているように思えます.
もし,ベクトルが規格化されていなかった場合,iが一致するところは 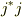 でその他は0の対角行列になりますが,
でその他は0の対角行列になりますが, 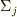 ということは,その対角行列を全てのjについて足し合わせろ,ということなのでしょうか?
ということは,その対角行列を全てのjについて足し合わせろ,ということなのでしょうか?
Re: ケットブラ?
カイ さんのレス (2007/12/07(Fri) 14:45)
書いていてわかったのですが,
もしかして,行列要素 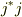 の部分を全て足し合わせると
の部分を全て足し合わせると
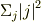
になって,これは波動関数の性質より,1になる. それで,対角行列を全てのjについて足し合わせると,単位行列になるってことですかね?
つまり,「行列の積の定義式に出てくるΣ」と「今考えているケットブラの式のΣ」は全く別のものであった.ということなのでしょうか?
Re: ケットブラ?
toorisugari no Hiro さんのレス (2007/12/07(Fri) 15:50)
> 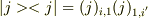 > で,もし規格化されていたのならば
>
> で,もし規格化されていたのならば
> 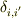 となります.
となります.
なりません. 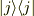 の
の 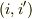 成分は
成分は 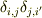 (
( 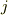 で和はとらない.)です.
# 演算子
で和はとらない.)です.
# 演算子 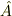 の
の 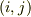 成分とは
成分とは 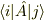 です.
です.
和をとってはじめて
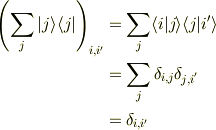
です.