量子力学の確率流密度問題

量子力学の確率流密度問題

tilfet さんの書込 (2007/11/23(Fri) 02:14)

はじめまして，tilfetといいます．シュレディンガー方程式から連続の方程式を利用して確率流密度

J=(h/2mi)×[P*∇P-(∇P*)P]…(1) （h:プランク定数にバーをつけたもの，*:複素共役）

を導く問題に関してわからないところがあるので質問させて頂きます．

この式を導く途中に出てくる，[(△P*)P-P*(△P)]…(2)を， 公式∇・(qR)=q∇・R+∇q・R…(3)を利用して ∇・[P*∇P-(∇P*)P]…(4)に変形する箇所で躓いています．

公式(3)の(q,R)に複素数である(P*,∇P)や(P,∇P*)が（内積の関係上）そのまま代入できるのかどうかがわからないのです．もし，公式(3)をそのまま適用したとすると，(2)式は， ∇・[P*∇P-(∇P*)P]-∇P*・∇P+∇P・∇P*…(5) となると思うのですが，Pは複素数なのでかける順序を入れ替えても複素共役になるだけで，最後から１項目と最後から２項目は同じ値にはならない…気が自分にはするのです．

参考書をいくつか調べてみたのですが，この部分はさらっと扱われていることが多くて，公式(3)をそのまま使っているのか，複素数の場合に(3)に似た自明な別の公式があってそれが暗黙のうちに使われているのか，単に自分が大きなカン違いをしているのか（これが一番ありそう…）が判断できません．

この部分がどうなっているのか，もしわかる方がいらっしゃいましたら，教えていただけると幸いです．

Re: 量子力学の確率流密度問題

toorisugari no Hiro さんのレス (2007/11/23(Fri) 19:43)

複素ベクトルの内積の問題ですね． 確かに，難しい問題です．ですが，計算では実ベクトル空間の内積(=ドット積)をそのまま流用すれば良いのです．大きさとか直交を考えるときだけ複素ベクトルであることを意識して複素ベクトル空間の内積で計算すれば，それ以外は実ベクトルの計算で大丈夫です．

スカラー値関数 f とベクトル値関数 \bm{v} に関して公式

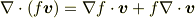
\nabla \cdot (f\bm{v}) = \nabla f \cdot \bm{v} + f \nabla\cdot\bm{v}

は複素数を体とするベクトル場(定義される空間は実3次元)でもそのまま成り立ちます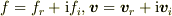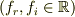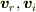． f=f_r+\mathrm{i}f_i, \bm{v}=\bm{v}_r+\mathrm{i}\bm{v}_i (f_r,f_i\in \mathbb{R}) , ( \bm{v}_r,\bm{v}_i は実ベクトル)として確かめてください．

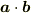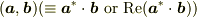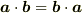ただし， \bm{a}\cdot\bm{b} はドット積であって，内積 (\bm{a},\bm{b})(\equiv\bm{a}^*\cdot\bm{b} \text{ or } \mathrm{Re}(\bm{a}^*\cdot\bm{b})) ではありません． ドット積は \bm{a}\cdot\bm{b}=\bm{b}\cdot\bm{a} を満たしますが，内積が満たすのは

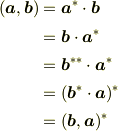
(\bm{a},\bm{b}) &= \bm{a}^*\cdot\bm{b}\\&= \bm{b}\cdot\bm{a}^*\\&= \bm{b}^{**}\cdot\bm{a}^*\\&= (\bm{b}^{*}\cdot\bm{a})^*\\&= (\bm{b},\bm{a})^*

です．

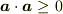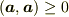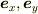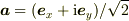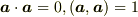ですから， \bm{a}\cdot\bm{a}\ge 0 は言えませんが， (\bm{a},\bm{a})\ge 0 は言えます．また，例えば \bm{e}_x,\bm{e}_y (実ベクトル)に対して \bm{a}=(\bm{e}_x+\mathrm{i}\bm{e}_y)/\sqrt{2} は \bm{a}\cdot\bm{a}=0, (\bm{a},\bm{a})=1 となります．大きさや直交を考えるときは内積で考えないといけません．

今回の問題は複素数値関数 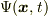\Psi(\bm{x},t) に関して (\triangle \Psi)^*\Psi- (\Psi)^*\triangle \Psi を計算すると言うことですが，そのまま，計算すればよいでのです．

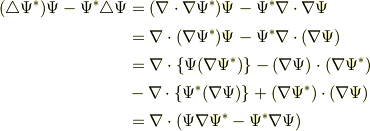
(\triangle \Psi^*)\Psi- \Psi^*\triangle \Psi &= (\nabla\cdot\nabla \Psi^*)\Psi - \Psi^*\nabla\cdot\nabla \Psi \\&= \nabla\cdot(\nabla \Psi^*)\Psi - \Psi^*\nabla\cdot(\nabla \Psi) \\&= \nabla\cdot\{\Psi(\nabla \Psi^*)\} - (\nabla\Psi)\cdot(\nabla \Psi^*)\\&- \nabla\cdot\{\Psi^*(\nabla \Psi)\} + (\nabla\Psi^*)\cdot(\nabla \Psi) \\&= \nabla\cdot(\Psi\nabla \Psi^* - \Psi^*\nabla \Psi)

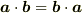最後の等式で \bm{a}\cdot\bm{b}=\bm{b}\cdot\bm{a} を使いました．

この問題では場が定義される空間が実3次元空間であることから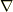， \nabla を実ベクトルとして扱っています．

Re: 量子力学の確率流密度問題

tilfet さんのレス (2007/11/24(Sat) 00:54)

詳しい解説どうもありがとうございます．

波動関数は複素数なのだから，ドットは複素数での内積なのだと勝手に思ってたことが行き詰まった原因だったみたいですね．（ついでに言えば，今の今まで，ドット積と内積が完全にイコールなものだと思ってました…）

値が複素数なのに，実数の時と同じ計算でOKというのはかなり不思議な気がしますが，とりあえず例のベクトル解析の公式が複素ベクトルでも成り立つことは確認できましたので，確率流密度の問題は無事なんとかなりました．

…が，大きさや直交のときと今回の場合で内積/ドット積と，扱いが異なるのには何か根本的な原因とか違いとかがあるのかどうか気になってきましたので，この点に関して再度質問してもよろしいでしょうか？

Re: 量子力学の確率流密度問題

toorisugari no Hiro さんのレス (2007/11/24(Sat) 12:41)

> 大きさや直交のときと今回の場合で内積/ドット積と，扱いが異なるのには何か根本的な原因とか違いとかがあるのかどうか気になってきましたので，この点に関して再度質問してもよろしいでしょうか？

これについてはきちんとしたお答えはできないと思います．

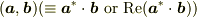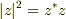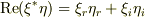内積が (\bm{a},\bm{b})(\equiv\bm{a}^*\cdot\bm{b} \text{ or } \mathrm{Re}(\bm{a}^*\cdot\bm{b})) と定義されるのは， |z|^2=z^*z あるいは \mathrm{Re}(\xi^*\eta)=\xi_r\eta_r+\xi_i\eta_i を考慮すれば理解できます．しかし，「何か根本的な原因とか違いとかがあるのかどうか」はうまく説明できません．そもそも，複素数自体，実2次元ベクトル空間と同型です．ですから，複素数を体とする3次元ベクトルが一筋縄ではいかないのは予想できると思います．

今回，場の定義域が実3次元ですからまだ簡単ですが，複素数多次元空間だとどんなになるかは私も知りません．

もし，関心があるのなら，リー群，リー環や複素多様体などを勉強してください．

Re: 量子力学の確率流密度問題

tilfet さんのレス (2007/11/24(Sat) 19:25)

回答ありがとうございます．

なにやら，非常にややこしそうな所に立ち入る質問をしてしまったようで済みません．さしあたり，この点はあまり気にしないほうが良さそうですね…．

toorisugari no Hiroさん，いろいろとありがとうございました．