円運動と摩擦力

円運動と摩擦力

ryomei さんの書込 (2007/11/12(Mon) 21:32)

初めまして，高校３年生です．

円運動について考えている内に自分の頭の中で勝手に問題提議してしまって混乱してしまいました，，

平らな（無限の広がりをもつとする）円盤の上に小物体を置きます． この円盤を等速円運動させます． この円盤と小物体に摩擦力が働くとしたらその摩擦力の大きさによってそれぞれどのような運動になるでしょうか？

摩擦力が 0 の場合は慣性系から見て静止 摩擦力が十分に大きいときは円盤に対して静止 となるのは分かるのですがその間がわかりません，どのような力が働きどのような軌道を描くのでしょうか？

少し話がそれますが 摩擦力 0 のときもそうだと思うんですが，慣性系から見て静止している物体を回転系からみると

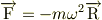
\overrightarrow{\rm F} &= -m\omega^{2}\overrightarrow{\rm R}

となりました．これは自分的にはとても不思議な結果でした（間違ってるかも 遠心力は常に円の中心から外側に働くものだと思っていたのですがそんなことはないんでしょうか？ それともこの結果は遠心力とは言わないのでしょうか

分からないことばかりで申し訳ないんですが，ご教示お願いします．

Re: 円運動と摩擦力

ミュフ猫 さんのレス (2007/11/12(Mon) 22:44)

ryomeiさん，こんばんは． 気のせいか，私が先に書き込むと，他の高レベルな方々が，書き込みを控えて しまわれるのが嫌なのですが・・・． 詳しく式で説明できません．感覚だけで予想します．ｗ

>この円盤と小物体に摩擦力が働くとしたらその摩擦力の大きさによって >それぞれどのような運動になるでしょうか？

徐々に回転速度を上げて，動き出す瞬間に回転速度を一定に保つとします． その瞬間において，向心力として小物体に働いていた最大静止摩擦力が， 突然無くなってしまうので，小物体は円運動の接線方向に飛ばされます． 動摩擦力が０ならば，そのまま等速直線運動すると思います． 回転系では，外側へ広がる渦巻き運動に見えると思います． 動摩擦力が０でないなら，慣性系でも等速直線運動にはならず，回転方向へ 曲がっていくような運動になると思います．

>それともこの結果は遠心力とは言わないのでしょうか？

言わないと思います．回転系の慣性力は二種類あり，遠心力とコリオリ力です． この場合は，遠心力の二倍の大きさのコリオリ力が真逆方向（つまり向心方向） に働くため，結果的に，慣性力の総和が小物体に働く向心力になるのだと思い ます．

Re: 円運動と摩擦力

ryomei さんのレス (2007/11/13(Tue) 00:49)

返信ありがとうございます．

ミュフ猫さんの言うとおりに徐々に回転速度があがると考えると納得いきました． ただ，いきなり速度を与えられた場合を考えたとすると微少の運動を考えなければならないと思うんですが， そうするとあると摩擦力が向心力の向かない気がします． 摩擦が０だとその場に停止することから考えて接線方向に働くような気がします．

でも今思うと小物体が円運動するということが既知でないとき，摩擦力が十分大きくても何故それが中心方向に向くかさえ分からないです，， 摩擦力が十分にあって回転系についていこうとするから，とかそんな感覚でいいんでしょうか？

僕も直感ではコリオリ力だと思ってたんですが， 慣性系から見て静止していない場合

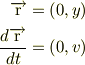
\overrightarrow{\rm r} &= \left(0,y\right) \\\frac{d\overrightarrow{\rm r}}{dt} &= \left(0,v\right)

としたときにこれを回転系でみると（ちょっと端折ります

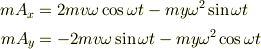
mA_{x} &= 2mv\omega \cos \omega t -my\omega^{2}\sin \omega t \\mA_{y} &= -2mv\omega \sin \omega t -my\omega^{2}\cos \omega t

となります． これを回転系の座標X,Yや速さVx,Vyに直したら僕の知ってる遠心力とコリオリ力の形になるんですが， 困ったことに計算するとこのmAx,mAyの第一項，第二項はバラバラ？になるんです． 静止の場合 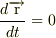\frac{d\overrightarrow{\rm r}}{dt} &= 0 とるからこのmAx,mAyの第一項が無い状態なので 数式上からみるとどっちとは言えないと思うんです