電荷間に働く力について
電荷間に働く力について
えり さんの書込 (2007/11/12(Mon) 13:57)
「一直線上の3点A,B,C上にそれぞれ 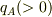 ,
, 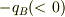 ,
, 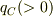 の点電荷が置かれている.これらの点電荷の間にはたらく力が互いにつり合うとき,
の点電荷が置かれている.これらの点電荷の間にはたらく力が互いにつり合うとき, 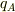 ,
, 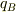 ,
, 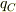 の間に
の間に
![\frac{1}{\sqrt[]{q_{A}}}-\frac{1}{\sqrt[]{q_{B}}}+\frac{1}{\sqrt[]{q_{C}}}=0](http://hooktail.maxwell.jp/bbslog/f57b941511f2f533fa99aa825eb5cf1b.png) の関係式が成り立つことを示せ.」
の関係式が成り立つことを示せ.」
という問題なのですが,このようになるときはそれぞれの電荷が等間隔に並んでいる必要があるのでしょうか.また,この式を証明するのに,
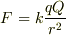 の式を使ってよいのでしょうか…
よろしくお願いします.
の式を使ってよいのでしょうか…
よろしくお願いします.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/12(Mon) 14:35)
ちょっと面白そうな問題ですね.
まず,3つ全ての点が2体力(2点間の距離の関数で決まる力)だけで相互作用するとします,クーロン力や重力はそうですね.これらの場合,明らかに,点と点との相互作用は3組しかありません.
また,問題は3つの点が,静止状態で釣り合うとしていると仮定します.
●ケース1:全て3組が引力か斥力の場合●
3点が運動をしない限り,密集してしまうか,バラバラになるかで,ある形状を保持出来るとはおもえません.
●ケース2:2組が引力で,他の1組は斥力の場合●
始めに,1つの平面内に適当な配置の状態を想定してみます;
<pre> -Q_B ● / 引力 / 引力 / / ○ーーーーーーーーー○ +Q_A斥力+Q_C </pre>
このままでは,釣り合えるとは思えません.点Aと点Cはどんどんと離れようとして,点Bは他の点に引っ張られるだけです.結局,平面内に3点を置いても,安定に釣り合う,三角形的な形状では安定して配置出来ないと推定出来ます.
結局,点Bは点Aと点Cとを結ぶ線上に来ないと安定しないと思います.
こう考えると,2体力の関数形は,必ずしも逆自乗形でなくとも良いのではないでしょうか.
例えば,点Aと点Cが棒で,点Bが強いバネ常数k_BAで点Aから引っ張られ,点Cが強いバネ常数k_BCで点Cから引っ張られた場合でも,同じように考える事が出来ますね.
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 14:36)
まだ,解いて確かめたわけではありませんが,,,
> という問題なのですが,このようになるときはそれぞれの電荷が等間隔に並んでいる必要があるのでしょうか.
そのようなことは記述されていないようです.
> また,この式を証明するのに, |13a35fc1ab3d12eab9d012b1cdbba494| の式を使ってよいのでしょうか…
力の向きさえ間違えないなら...
一般的な位置を与えて解けばいいのですが,並進対称性を利用して,一個の位置を簡単なものにすれば,計算が楽で見通しが良くなると思います.
非線形だから,いけるかどうかわかりませんが,行列式に持ち込むのが定石です.
P.S.
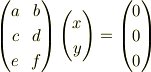
に対して 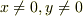 が存在するには,
が存在するには, 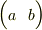 ,
, 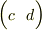 ,
, 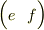 がすべて平行(同一直線上)という議論ですね.
がすべて平行(同一直線上)という議論ですね.
P.S.2 たぶん次は釣り合いの位置からのズレの方程式を線形近似でもとめて,3個のノーマルモードに展開するという流れでしょうか?
Re: 電荷間に働く力について
tip★ さんのレス (2007/11/12(Mon) 17:36)
>>このようになるときはそれぞれの電荷が等間隔に並んでいる必要があるのでしょうか.
つり合いの式を解いていけば分かると思いますが,電荷間の距離は消えるので考える必要はありません.
だから, 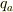 と
と 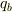 ,
, 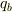 と
と 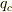 の距離を1として考えてみれば簡単だと思います.(これって反則かな??)
の距離を1として考えてみれば簡単だと思います.(これって反則かな??)
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 18:27)
> 電荷間の距離は消えるので考える必要はありません.
電荷間の距離の比は残りますよ.
> だから, |f268473b78983af44d67c82031d84a55| と |38136407ede268c1097dea71d41a28e8| , |38136407ede268c1097dea71d41a28e8| と |5d458086f12554ef65b23a329a026713| の距離を1として考えてみれば簡単だと思います.(これって反則かな??)
たぶん, 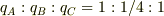 に限定されると思います.
# tip★さんのおっしゃるとおり1/4ですね.
に限定されると思います.
# tip★さんのおっしゃるとおり1/4ですね.
Re: 電荷間に働く力について
tip★ さんのレス (2007/11/12(Mon) 18:57)
>>電荷間の距離の比は残りますよ.
自分の考えではどう考えても残らないのですが・・・
あと1:4:1にしたら,上の式は成り立たないと思います. 4:1:4ならわかりますが.
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 19:09)
> 自分の考えではどう考えても残らないのですが・・・
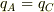 がでますよ.
がでますよ.
# そもそも行列の0固有ベクトルが任意なら,行列は0行列になります.
> 4:1:4ならわかりますが.
その通りです.訂正しました.
Re: 電荷間に働く力について
tip★ さんのレス (2007/11/12(Mon) 19:20)
>> 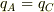 がでますよ.
がでますよ.
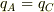 は本当に成り立ちますか?
もし,9:4:36にしたら上の式を満たしますよ.
行列で考えてないから話があわないのかな・・・
は本当に成り立ちますか?
もし,9:4:36にしたら上の式を満たしますよ.
行列で考えてないから話があわないのかな・・・
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 19:44)
> だから, 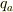 と
と 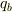 ,
, 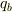 と
と 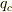 の距離を1として考えてみれば簡単だと思います.
の距離を1として考えてみれば簡単だと思います.
> もし,9:4:36にしたら上の式を満たしますよ.
本当に? 直感にも合わないですよ.
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 19:51)
tip★さん, とりあえず,ペンディングにしましょう. そうでないと,えりさんを置いてけぼりにしてしまします.
えりさんが方程式を書いてくれたら,そこから議論を再開しましょう.
Re: 電荷間に働く力について
tip★ さんのレス (2007/11/12(Mon) 20:11)
すいません,距離の比は残りますね.読み間違いしていました. 自分が言いたいのは,電荷の大きさを色々変えれば,距離はどうとでもなるということです. あと,9:4:36は成り立つと思います.距離を1:2にすれば
また,ずっと1:1で考えているわけではありません.
最初に1:1でやってみてください.といったのは,別に545354:655や123:546などの適当な比を使っても別にかまわない.という意味です.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/12(Mon) 20:26)
難しい計算の論議になっているようですが,簡単に話を進めてみます.
私の意見では,難しい計算をする事なしに,静的安定解は,点A,B,Cが一直線のばあいしかあり得ないとおもいます.そこで,仮に内側の点Bからみた,点A,Cまでの距離を 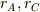 とします.
とします.
まず,点Bでのクーロン・力の平衡から,

同様に,点Aでのクーロン・力の平衡から,
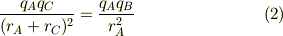
点Cについては,上記の式と重複するので省略します.
式(1)から直ちに,

式(2)で 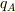 を辺々消去して,逆数の平方根を取ると;
を辺々消去して,逆数の平方根を取ると;
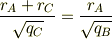
整理して,式(3)を代入すれば,
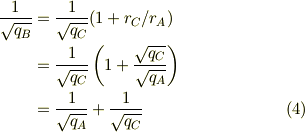
となりますね.あくまでクーロンの力による静止平衡の式から出すべきで,先験的に間隔を決めるというのは,物理的な考え方に反するものだと思いますよ.
この問題で面白いのは,AとCの電荷の比は自由に替えても間隔の比が式(1)ないしは式(3)で決まるだけでなく,中間の電荷が,一種の平均値みたいな値に限定されることですね.
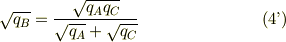
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 20:33)
あああああ,zoroさん答え書いちゃった.
Re: 電荷間に働く力について
tip★ さんのレス (2007/11/12(Mon) 20:40)
>>zoroさん
上の式が,距離の比1:1であっていても,それ以外の無限にある距離の比のことを議論していないから駄目ということですよね. それは分かっているつもりだったんですど,自分の日本語力不足です. 自分国語へたれですから.
Re: 電荷間に働く力について
ミュフ猫 さんのレス (2007/11/12(Mon) 20:40)
おお!なるほど!等間隔じゃなくてもいいんだな・・・.
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 20:57)
zoroさんがフライングしちゃったので,あきらめてかきます. (釣り合いの式をたてるところが峠だったのに....)
並進対称性より,すべての点を平行移動しても一般性は失われない.
よって,
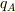 のx座標を
のx座標を 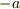
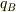 のx座標を
のx座標を 
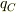 のx座標を
のx座標を  とおく.ただし,
とおく.ただし, 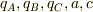 は正とする.
は正とする.
このとき,釣り合いの式は
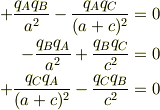
正値の条件から
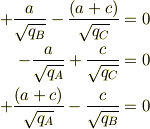
行列の形に書けば,
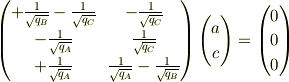
前述(No.18579)の考え方により非零の 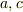 が存在する必要十分条件は
が存在する必要十分条件は
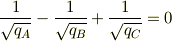
また,0固有ベクトルは 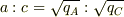 を満たすものとなる.
を満たすものとなる.
# もちろん,行列に持ち込まないでやった方が初学者には簡単ですが,後を考えてこの方法も理解しておきましょう.強力です.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/12(Mon) 21:33)
敢えて,物理の論議の進め方について意見します.
この問題は,自分が見た事も,聞いた事もなかったのでとても興味深く感じたので,大雑把な考え方を書かせて頂きました.でも,本当に直線型の配置しか存在するかしないかは,私には難しすぎる問題と思いました.
いずれにしろ,いくつかの意見を基にえりさん,ご本人の計算を待っていたつもりです.
ところが,式が不明確なまま,距離の具体的な比の論議が始まったのを拝見して驚愕しました.判っている人には,参考意見を書かれているおつもりでしょうが,私も含めて,式を検討していない人々に取っては,チンプンカンプンのお話です.
あまつさえ,最初のご質問で; >このようになるときはそれぞれの電荷が等間隔に並んでいる必要があるのでしょうか.
と述べられていることを考えると,「数字のセット」の善い悪いと行った論議はとても誤解を招くだろうと拝察しました.
従って,急遽,直線状に配置した,クーロン力に従った静止条件の式を書き下し,自分の見解を付けてみました.
他方,難しい計算は判りませんが,大学1年生の論議には,直裁な式の展開と,そこからえられた解の特徴を理解する事が大切だと思います.
勿論,学年が進むにつれて,物理数学の広い知識に照らし合わせて,更に深い分析や考え方をする事に反対ではありません.むしろ若い方々にはアドバンストな物理にドンドン挑戦して戴きたい者です.
しかし,この問題のように基礎的な問いに,あまりにも細かすぎるヒントをいくら書かれても,かえって誤解を生みだす危険性を感じます.
私は,物理の問題を出されたとき,その「答え」をいくら聞いてもあまり価値がないと考えています.むしろ,その答えを出すにいたる「考え方」や「その答えについての解釈」が理解されない限り論議の価値が低いだろうと思います.
以上,落ちこぼれ老人の一意見です,ご参考まで.
でも,論議は活発に進まれて下さいね.
Re: 電荷間に働く力について
ミュフ猫 さんのレス (2007/11/12(Mon) 21:57)
>以上,落ちこぼれ老人の一意見です,ご参考まで.
ええ?そ,そんなお年だったんですか? 失礼ですが,てっきり30歳くらいと思ってました.(^_^;)
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/12(Mon) 22:00)
> でも,本当に直線型の配置しか存在するかしないかは,私には難しすぎる問題と思いました.
問題をよめば一目瞭然です. 2次元のことはzoroさん以外,誰も触れていません.
> 他方,難しい計算は判りませんが,大学1年生の論議には,直裁な式の展開と,そこからえられた解の特徴を理解する事が大切だと思います.
ええ.ですから,この問題の山は釣り合いの式を書くことです.そこから先は些末です.
釣り合いの式を書かれてしまっては,えりさんがどこで詰まっているか理解されていないと思われてもしかたないのでは?
Re: 電荷間に働く力について
tip★ さんのレス (2007/11/12(Mon) 22:54)
全ての原因は自分の安易な発言にあると思います. もうちょっと良く考えてから書き込むようにします.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/12(Mon) 23:04)
>力の向きさえ間違えないなら... > >一般的な位置を与えて解けばいいのですが,並進対称性を利用して,一個の位置を簡単なものにすれば,計算が楽で見通しが良くなると思います. > >非線形だから,いけるかどうかわかりませんが,行列式に持ち込むのが定石です.
最初のご意見の部分を引用させて戴きました.もとの力学的方程式が出てこない段階で,このご意見はなにを示しているのか,とても疑問でした.高度な数学的な理解が進めば,流れるように繋がったお話だろうとは推察していますが.
少なくとも,私が学部1年生のときに,お説を拝見したら,この問題に取り組む意欲が失せそうです.
>問題をよめば一目瞭然です. >2次元のことはzoroさん以外,誰も触れていません.
それでしたら,行列式の計算で何を証明した事になるのですか?
もしその様な計算をするなら,二次元平面で「解は直線しか無い」証明をするべきで,すでに力学的平衡の式からえられた結論を再度得ても,どのような物理的意味が付与されたか理解出来ません.
>釣り合いの式を書かれてしまっては,えりさんがどこで詰まっているか理解されていないと思われてもしかたないのでは?
それこそ,逆ではないですか.質問者さんが「式が立たない」からこその質問です.それを置き去りにして,「具体的な数字」を云々していたら,それこそ一体なんだろうと思われないでしょうか?
勿論,必要な式を立てたあとで,簡単な具体例でチェックするとかはあるでしょう.でも,いまの段階では式が出ていないで,誤解されませんか?
やはり,問題の重要論点を論じて,相互理解が深まるにつれ,関連事項や高度な解析などの問題に進むべきだろうと思います.幾ら何でも,「並進対称性」を意識しないでも,点Bを原点として考えるのは至極当然です.数学的厳密正の重要性も大事でしょう.しかし,初学者は「物理的直感に裏付けられた式の運用」を直裁に行えるべきで,「あまりにも仔細なことは意識して無視するべき」ではないでしょうか?
もちろん,物理数学的な厳密な考え方は,そのような「ナイーブな力」を基盤として新価を発揮すると感じます.手法としての物理数学が判っても,適応する基盤がグラグラだと物理数学的知見が意味をなさないように思います.
此れまでの経験で,これ以上論議しても堂々巡りと思いますし,常日頃の高度なご意見は参考にさせて頂いています.ただただ,もう少し質問者さんの目線から解説をお願いするのみです.
後は,えりさんの質問攻勢を楽しみにしています.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/12(Mon) 23:26)
tip★さん,
>全ての原因は自分の安易な発言にあると思います. >もうちょっと良く考えてから書き込むようにします.
あ,そんな事はありません.むしろ,
>>>このようになるときはそれぞれの電荷が等間隔に並んでいる必要があるのでしょうか.
>
>つり合いの式を解いていけば分かると思いますが,電荷間の距離は消えるので考える必要はありません.
>だから, 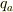 と
と 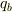 ,
, 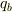 と
と 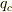 の距離を1として考えてみれば簡単だと思います.(これって反則かな??)
の距離を1として考えてみれば簡単だと思います.(これって反則かな??)
これは,面白いヒントになると思いましたよ.これに対してのえりさんの再質問に興味がありました.
その意味では,「比」が主役という面白い問題だったのでしょうか.
論戦は「語学と一緒で,する程に色々な能力に磨きが掛かる」と思います.為には,失敗を恐れずに,自分のフィーリングに従って,ドンドン発言されることを期待します.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/12(Mon) 23:31)
ミュフ猫さん,
>ええ?そ,そんなお年だったんですか? >失礼ですが,てっきり30歳くらいと思ってました.(^_^;)
大変お恥ずかしい事に,もうすぐその倍の歳になります.
この数式掲示板のお陰で,惚けた頭がかなりリフレッシュできました(笑).
Re: 電荷間に働く力について
えり さんのレス (2007/11/13(Tue) 15:37)
遅れてすみません.
私がどこで詰まっていたかというと,B点にばかり目がいってしまい,A点やC点のつり合いを考えていなかったことです.
ですので,式は
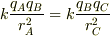 までしか立たず,一つの式の中に未知数が2つあるので困ってしまい,3つの電荷が等間隔に並んでくれれば
までしか立たず,一つの式の中に未知数が2つあるので困ってしまい,3つの電荷が等間隔に並んでくれれば  が消えるのになあ,と浅はかに考え,初めのようなことを質問した次第です..
が消えるのになあ,と浅はかに考え,初めのようなことを質問した次第です..
それから,行列に書き換えて考えるほうが後々役立つということでしたが,現段階では,私の中で「行列」と「物理の問題」はまだ繋がっていないので,理解に苦しみそうです.学校ではまだ本格的な行列式や固有値ベクトルの勉強はしていないので,追々習得できるようにしたいと思います.
基礎的な質問で申し訳ありませんでした. これからも宜しくお願いします.
Re: 電荷間に働く力について
zoro さんのレス (2007/11/13(Tue) 18:58)
>私がどこで詰まっていたかというと,B点にばかり目がいってしまい,A点やC点のつり合いを考えていなかったことです.
大学に入っても,問題を「絵」にするのは,やはり「問題を第三者的に見る」為の善い武器だとおもいます.
特に,なにか不思議な状態に陥ったら,「絵」ですね.私のノートは「方眼罫」の為に絵をすぐに書き込めます.それを見ながらPCに式を打ち込みます.
#PCに向かって,絵を打ち込めると善いのですが....
で,三電荷の絵を見ていたら,四電荷だとすると平面配置の平衡があるような気がして来ました(笑).
Re: 電荷間に働く力について
toorisugari no Hiro さんのレス (2007/11/14(Wed) 09:49)
>問題をよめば一目瞭然です. >2次元のことはzoroさん以外,誰も触れていません.
> もしその様な計算をするなら,二次元平面で「解は直線しか無い」証明をするべきで,すでに力学的平衡の式からえられた結論を再度得ても,どのような物理的意味が付与されたか理解出来ません.
簡単に. 「2つの力が釣り合うのなら,ふたつの力は平行」あるいは「ふたつのベクトルが一次従属なら平行」