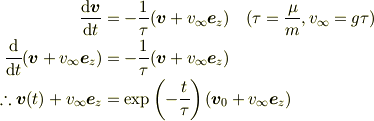空気抵抗のある水平投射
空気抵抗のある水平投射
yaj さんの書込 (2007/11/06(Tue) 22:36)
お久しぶりです. 高2です. 現在空気抵抗のある水平投射を考えています.
質量  の球を,高さ
の球を,高さ 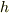 の台から初速度
の台から初速度 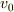 で水平投射をします.
空気抵抗は飛行速度
で水平投射をします.
空気抵抗は飛行速度  に比例(比例定数を
に比例(比例定数を  とする)するとします.
とする)するとします.
縦に  軸(上が正),横に
軸(上が正),横に  軸(右が正)をとり,投射前の球の位置は(0,h)とします.
軸(右が正)をとり,投射前の球の位置は(0,h)とします.
そうすると,  秒後の球の座標は
秒後の球の座標は
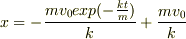 …(1)
…(1)
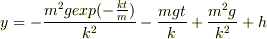 …(2)
…(2)
となるはずです ( http://www12.plala.or.jp/ksp/mechanics/resistdown/ を参考にしました)
これから,t秒後にy=0となる(球が着地する)ときのx座標を求めます.
(1)を変形して
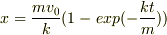 …(3)
(2)にy=0を代入して変形してtについて解くと
…(3)
(2)にy=0を代入して変形してtについて解くと
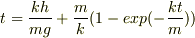 …(4)
(4)に(3)を変形した値を代入すると
…(4)
(4)に(3)を変形した値を代入すると
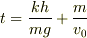
(----修正:上の式ではなく
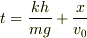 です.
打ち間違いをしていました.ご指摘ありがとうございました)
です.
打ち間違いをしていました.ご指摘ありがとうございました)
これを変形すると
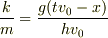 ,
, 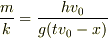 …(5)
(3)に(5)の値を代入すると
…(5)
(3)に(5)の値を代入すると
![x=\frac{hv_0^2}{g(tv_0-x)}[1-exp(-\frac{g}{hv_0}(v_0t^2-tx))]](http://hooktail.maxwell.jp/bbslog/6caab700e033cef527e939b18c1658f4.png)
実験結果より,
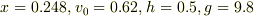 がわかっているのでこの値を代入すると
0.248*9.8=0.5*0.62*0.62*(1-exp(-19.6*t^2+7.84*t))/(0.62*t-0.248)
がわかっているのでこの値を代入すると
0.248*9.8=0.5*0.62*0.62*(1-exp(-19.6*t^2+7.84*t))/(0.62*t-0.248)
ここからが問題なのですが(それ以前が間違っていたら元も子もありませんが…)
これを満たすtを,グラフを使って解くと(maximaを使いました) tは大体 0.28,0.4 のあたりの値になります(かなりアバウトです) しかし,t=0.4では,与式を除算することになってしまう(0.62*t-0.248の部分です)ので,t=0.4の方は不適切であることがわかります よって,t=0.28
・・といいたいところなのですが,
空気抵抗がない状態で高さ0.5から(今回の水平投射と同じ高さです)球を自由落下させる場合の所要時間は明らかに
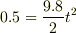 t≒0.32
t≒0.32
これによれば,空気抵抗があるほうが空気抵抗がない時より物体が着地するまでの時間が短いというなんとも恐ろしい結果になってしまいます.. しかも空気抵抗係数kが負の値になってしまいます..
かなり長くなりましたが,どこが間違っているのがご指摘いただけましたら,どうかよろしくお願いします. (また恥ずかしい間違いをしていなければよいのですが)
Re: 空気抵抗のある水平投射
yama さんのレス (2007/11/07(Wed) 08:43)
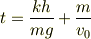
はおかしいと思います.右辺の第2項は時間の次元を持ちません. と思いましたが
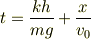
の単なる書き間違いのようですね.
>しかし,t=0.4では,与式を除算することになってしまう(0.62*t-0.248の部分です)ので,t=0.4の方は不適切であることがわかります
分母が0になるから不適切ということでしょうか? しかし,このときは分子も0になるので,極限値をとれば式は成り立つと思います. 従って t=0.4 としてよいと思います.
Re: 空気抵抗のある水平投射
yaj さんのレス (2007/11/07(Wed) 18:01)
返信ありがとうございます. 確かに分母が0になり,t=0.4でも成立しそうです.
しかし,上の(1) (2)の式に実験値とt=0.4を代入すると
0.248=-0.0083*0.62*exp(-k*t/0.0083)/k+0.0083*0.62/k…(1)' 0=-0.0083^2*9.8*exp(-k*t/0.0083)/k^2-0.0083*9.8*t/k+0.0083^2*9.8/k^2+0.5 …(2)'
となりますが, (2)'から k=0.03175561141999715 という値が出るにも関わらず, (1)'からはk=0.0000… といった値になり(2)'の値と全く一致しません… (勿論,(2)'に(1)'で出たkの値を代入しても等式は成り立ちません)
実は,式変形をする以前の(1),(2)の段階で計算間違いをしているのでしょうか? どうも挫折気味です..
Re: 空気抵抗のある水平投射
yama さんのレス (2007/11/07(Wed) 19:08)
t=0.4 はやはり不適切のようです.その理由は分母が0になるからというよりも,k=0 になるからです.k=0 ということは空気抵抗がないということなので,t=0.32 となり矛盾が生じます. しかし,だからと言って(1),(2)の段階で間違いがあるとは言えません.最後の式が(1),(2)から導かれるとしても,逆は必ずしも成り立たないからです.
ところで,実験値に間違いはないのでしょうか. 水平到達距離が空気抵抗の無い場合よりも大きくなっているのはどうかな?と思います.
Re: 空気抵抗のある水平投射
toorisugari no Hiro さんのレス (2007/11/08(Thu) 02:41)
よこからすいません.
> ところで,実験値に間違いはないのでしょうか.
これが本当に実験値なら,かえってまずいかもしれません.なぜなら,空気抵抗が速度に比例するのはレイノルズ数が非常に小さいとき,つまり,非常に速度が小さいか,物体が非常に小さいか,液体(気体)の粘り気(粘性)が非常に大きい場合しか成り立ちません.
# 空気中を水滴が落下する場合直径0.1mmより小さくないとダメです.(ほとんど浮遊している状態)
そうでないときは,空気抵抗はだいたい速度の2乗に比例します.
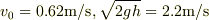 という速度の大きさを考えると,その可能性が高いと思います.
という速度の大きさを考えると,その可能性が高いと思います.
終端速度を  ,物体の直径を
,物体の直径を  とすれば
レイノルズ数は
初期
とすれば
レイノルズ数は
初期 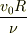 ,後期
,後期 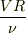 で与えられます(ただし,
で与えられます(ただし, 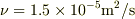 は空気の動粘性率).計算して,ぞれぞれ,1より小さいことを確かめてください.
は空気の動粘性率).計算して,ぞれぞれ,1より小さいことを確かめてください.
# もっとも,「水平到達距離が空気抵抗の無い場合よりも大きくなっているのはどうかな?」なので,データや計算の信頼性自体がない可能性も高いですが... # それともトップスピン....
Re: 空気抵抗のある水平投射
yaj さんのレス (2007/11/08(Thu) 06:10)
実験は,下のHPのように(どこかの高校のHPみたいです),滑り台の上から金属球を落とす→ガラス球と衝突させる→運動量保存を確認する
みたいな感じのものでした(詳しくは読んでいませんが,装置は図と同じでした).
そのとき,金属球をガラス球と衝突させなかった場合の発射速度を計測器ではかり(その値が0.62m/sとなりました),飛行距離を計ったところ,x=0.248m となりました(実験は5回行いました.毎回ほぼ同じ値を示しました)
それで,最初は空気抵抗がない場合の水平投射の公式を用いて実験値と理論値を比較したところ,実験値が大きく上回ったので,
これは,「物体が空気抵抗を受けたことにより,飛行時間がのび,その結果飛行距離が伸びたのではないか」という仮定(今考えるとかなり胡散臭い仮定です)をたて,空気抵抗が速度に比例すると仮定した上で,上に示した計算を行ったところ… 大変なことになりました(笑)
球の半径はたしか2cm位だったと思うので, 初期のレイノルズ数は 826.66666… ということで1を大きく(!)上回っています(終端速度はありません)
ということでそもそも空気抵抗に比例するという仮定が間違っていたようです..
レポートには(今日が提出日なので),速度計が間違っていた(または計り方が間違っていた)か,抵抗が速度に二乗する(どうもこれは原因である可能性が低そうですが)か,何か他の原因があった,とでも書いておくことにします.
どうもありがとうございました.
Re: 空気抵抗のある水平投射
toorisugari no Hiro さんのレス (2007/11/08(Thu) 11:45)
> (または計り方が間違っていた)
速度計が速度に対して正しい方向に設定されていなくて,速度を少な目に計測したのではないかな?
> 初期のレイノルズ数は 826.66666…
なかなか素敵な数ですね.日常よく現れるレイノルズ数 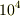 〜
〜 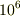 にくらべると小さいですが,しっかり流れが乱れていて,とても速度に抵抗は比例はしませんね.
にくらべると小さいですが,しっかり流れが乱れていて,とても速度に抵抗は比例はしませんね.
>(どうもこれは原因である可能性が低そうですが)
抵抗をいれても距離が延びる説明にはなりませんね.それに,密度が大きい物体の様ですから,慣性に比べ抵抗はあまり大きくなさそうです.
> 大変なことになりました(笑)
これが実験の醍醐味でしょう:-)
Re: 空気抵抗のある水平投射
zoro さんのレス (2007/11/09(Fri) 02:23)
横から失礼します.
高校生さんとすると,複雑な計算は許されないのかも知れませんが,大雑把な考えかたの一つをすこし書いてみます.なお,私は微分方程式を解くのが苦手なので,いま現在,詳しい解を知りませんが....
時刻,t=0から水平に飛び出した球の,ある時刻t>0での速度ベクトルを 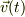 ,その早さを
,その早さを 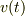 ,x軸となす角を
,x軸となす角を 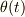 とします.
とします.
![\vec v(t) = v(t)*[\cos(\theta(t))\vec e_x -\sin(\theta(t))\vec e_y] \tag{1}](http://hooktail.maxwell.jp/bbslog/43bc0d751cff126352285d487a47d8ff.png)
この式の微分は成分毎に丁寧に,陰関数の微分をすれば求められる筈ですね.でも,お爺さんは三角関数が苦手なので,

と置き換えて,複素数平面に移行します.とすると,オイラーの公式; 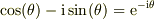 ;により三角関数が消えて,とても簡単になります.高校で習わないのでしょうが,雰囲気だけ見て下さい.
;により三角関数が消えて,とても簡単になります.高校で習わないのでしょうが,雰囲気だけ見て下さい.
さて,式(1)の左辺部のベクトルを複素数に変換した結果を 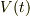 としますと,
としますと,
![V(t) &= v(t)*[\cos(\theta(t))(1) -\sin(\theta(t))(\mathrm{i})] \\&= v(t)\mathrm{e}^{-\mathrm{i}\theta(t)} \tag{1'}](http://hooktail.maxwell.jp/bbslog/1740b6d8dd77a6890ebc24b722c01d93.png)
とコンパクトな表現になります.ここで,初期条件は,題意より,
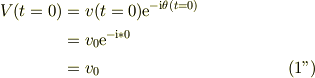
です.
加速度を求めるには式(1')を時間について微分するだけです.「実関数の指数関数」の微分と同じように,「指数部分に虚数が入っているだけ」と考えれば,微分も簡単に出来て,
![\dot V(t) &= \dot v(t)\mathrm{e}^{-\mathrm{i}\theta(t)} +v(t)[-\mathrm{i}\dot \theta(t)]\mathrm{e}^{-\mathrm{i}\theta(t)} \\&= [\dot v(t) -v(t)\dot \theta(t)\mathrm{i}]\mathrm{e}^{-\mathrm{i}\theta(t)} \tag{3}](http://hooktail.maxwell.jp/bbslog/1b1bb282eaf426bfb5faf455a1695eca.png)
となります.
他方,運動方程式は,
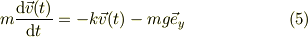
ここで,式(2)の単位ベクトル→(1,i)の変換を適用すると,式(1)→式(1)'と同様に,運動方程式も複素数表示が出来て,
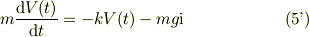
辺々を球の質量, 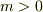 で割り,整理すると,
で割り,整理すると,
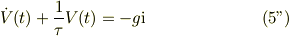
ここで,緩和時間として,

式(5'')に式(3)を適用すれば,複素数表現の運動方程式;
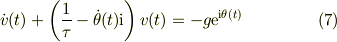
となります.運動方程式が1本のように見えるのは,複素数の方程式なので,実部,虚部に分けて書くと;
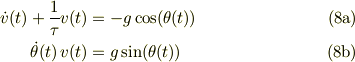
となると思います.具体的な条件に従って,上記の連立微分方程式によって球の運動が決まると考えると良いのでしょう.
恐らく,初速 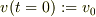 と重力加速度
と重力加速度  との比などで,近似条件を考えて,段階的に計算を進めるのだろうと思います.
との比などで,近似条件を考えて,段階的に計算を進めるのだろうと思います.
なお,ある時刻,tでの位置は;
![x(t) &= \int_{t'=0}^{t'=t}v(t')\cos[\theta(t')]\mathrm{d}t' \tag{9a}\\y(t) &= h - \int_{t'=0}^{t'=t}v(t')\sin[\theta(t')]\mathrm{d}t' \tag{9b}](http://hooktail.maxwell.jp/bbslog/2302d3a1d66b67225f9f3156dda23a4b.png)
具体的な計算は,まだ出来なくてご免なさい.数学に強い方々の助太刀を求めます.きっと,色々な解き方があるように感じます.
Re: 空気抵抗のある水平投射
yama さんのレス (2007/11/09(Fri) 10:57)
運動方程式を解いて時刻tの位置を具体的に表すと,yajさんが最初に書かれた(1),(2)式になるのだと思います. この式を用いていろいろなk/mの値について運動経路を計算すれば,その中から実験値を満たすk/mの値を見つけることができるはずですね. ところが実験値を満たすk/mの値は負になってしまったというわけです. 確かにk/mの値が負であれば,速度に比例する力で加速されるので,より短時間で,より遠くに着地することになりそうです. しかし,熱力学第2法則を考慮すればk/mが負になることはないでしょう.
そうなると,運動方程式が正確でないか実験値に誤差がある可能性が考えられますが,それについてはtoorisugari no Hiroさんの考察が的を射ていると思います.
Re: 空気抵抗のある水平投射
zoro さんのレス (2007/11/09(Fri) 23:31)
>運動方程式を解いて時刻tの位置を具体的に表すと,yajさんが最初に書かれた(1),(2)式になるのだと思います.
しかし,運動方程式が明示されないまま,解だけが示されても,その是非を論議出来ないのではないでしょうか.
ふつう,エネルギ散逸が早さの関数で,速度の方向の逆向きである限り,早さの関数形にはあまりシビアに影響されないと思います.勿論比例係数は,実験に合わせる為に流体力学的な意味を論議するなら別問題だとおもいます.また,係数が正になるのは明らかに異常だとおもいます.
Re: 空気抵抗のある水平投射
toorisugari no Hiro さんのレス (2007/11/10(Sat) 00:17)
> ふつう,エネルギ散逸が早さの関数で,速度の方向の逆向きである限り,早さの関数形にはあまりシビアに影響されないと思います.
ちょっと,暴論に聞こえます.
無限遠で0になる減少関数だから同じと見なせるとおっしゃっているように聞こえます.
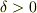 として,速さの
として,速さの 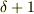 乗に比例し,速度に逆向きの抵抗の場合,速度は減少はするけど「減衰」はしません.
乗に比例し,速度に逆向きの抵抗の場合,速度は減少はするけど「減衰」はしません.
long time tailという言葉をご存じでしょうか?
Re: 空気抵抗のある水平投射
toorisugari no Hiro さんのレス (2007/11/10(Sat) 00:52)
ついでに,一様重力と速度に比例する空気抵抗の下での斜方投げ上げ問題をベクトルでやってみます.基本的に一次元の場合と一緒です.
 軸を鉛直上向きにとります.質量
軸を鉛直上向きにとります.質量  ,重力加速度の大きさを
,重力加速度の大きさを  ,空気抵抗係数を
,空気抵抗係数を 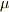 とすると,速度
とすると,速度 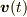 が満たす微分方程式は
が満たす微分方程式は
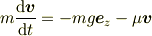
となります.これを変形すると,解は,
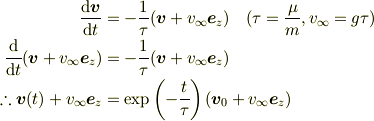
です( 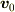 :初期速度).位置の計算も基本的に指数関数の積分です.
:初期速度).位置の計算も基本的に指数関数の積分です.
簡単なのは線形方程式だからですね.速度の2乗に比例する場合,非線形の2次元常微分方程式系(3次元速度ベクトルでも)ですから,私は一般的に解けるか知りません.
Re: 空気抵抗のある水平投射
zoro さんのレス (2007/11/10(Sat) 02:09)
>> ふつう,エネルギ散逸が早さの関数で,速度の方向の逆向きである限り,早さの関数形にはあまりシビアに影響されないと思います. > >ちょっと,暴論に聞こえます. > >無限遠で0になる減少関数だから同じと見なせるとおっしゃっているように聞こえます.
粗い論議だとは思いますが,暴論ではないと感じています.
水泳で「蹴伸び」といって,プールの側面を蹴って進む距離を長くするように練習します.その一次元解析では,早さに正比例型でも,早さの自乗に比例型でもパラメータを適切にすれば,距離と時間の関係は正のパラメータで決まりました.
球の問題でも,厳密な理論計算から早さの関数形を与えられない限り,それほど関数形に拘る必要はないと思います.
水泳の話が出ましたが,人間が流線型ぽい姿勢,ストリーム・ラインと呼ばれますが,この時の抵抗は,体重・身長などのパラメタとv^m, m=2.3とかいった解析を見た記憶があります.その時は,m=2にしておいてもいいのではと思ったものです.
> 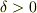 として,速さの
として,速さの 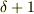 乗に比例し,速度に逆向きの抵抗の場合,速度は減少はするけど「減衰」はしません.
乗に比例し,速度に逆向きの抵抗の場合,速度は減少はするけど「減衰」はしません.
全く理解出来ません.もうすこし噛み砕いてご説明お願い出来ますか?
>long time tailという言葉をご存じでしょうか?
これも不勉強で存じません.上と関係があれば,知りたい所です.
Re: 空気抵抗のある水平投射
toorisugari no Hiro さんのレス (2007/11/10(Sat) 02:31)
線形抵抗がどの速度域でも発生しないのなら,特に全速度域で抵抗が「速さ」の2乗に比例するのなら,減速はするけど,いつまで経っても止まりません.
> 全く理解出来ません.もうすこし噛み砕いてご説明お願い出来ますか?
速度スケールの 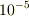 以下になれば静止と考える場合,普通は10「時間スケール」程度ですが,上のモデルだと
以下になれば静止と考える場合,普通は10「時間スケール」程度ですが,上のモデルだと 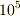 「時間スケール」程度かかります.
「時間スケール」程度かかります.
詳しくは微分方程式
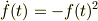
を解いて,
あと,放射性物質の個数の時間依存性が 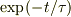 になる場合,「平均寿命」は
になる場合,「平均寿命」は  ですが,
ですが, 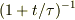 になる場合,「平均寿命」は無限大になること(long time tail)を確かめられればわかります.
になる場合,「平均寿命」は無限大になること(long time tail)を確かめられればわかります.
ま,もっとも,実際の解析の場合,形状と粘性率,質量から決まる「限界速度」以下の速度は0とすれば,あるいは,そこからは線形抵抗に切り替えれば,何も問題はありません.たいていの場合,限界速度はスケールに比べほとんど0に近いですから.
そういう意味で,zoroさんのおっしゃることに大筋で間違いはないのですが,「散逸」形態が一緒と読めるのにひっかかっただけです.
Re: 空気抵抗のある水平投射
zoro さんのレス (2007/11/10(Sat) 13:30)
まだ仰る事が良くわからないのですが,
>詳しくは微分方程式
>  >を解いて,
>を解いて,
これを拝見していて,水泳の蹴伸びを検討した時の記憶がすこし蘇ったので,コメントします.
水泳でも,トップ・スイマーは,「早さ,v」の自乗の抗力を受けると言われています.ストリーム・ライン姿勢では,一次元近似で;
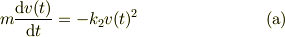
此れに対して,線形の抗力では,
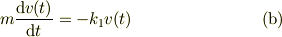
式(b)については,物理系の学生ならば,指数的な振る舞いをするのはピンときます.ところが,式(a)は非線形であり式(b)より大きな抗力だから,有限時間でストップすると考え,式(b)でモデル計算をしていました.
あるとき,小さな早さ領域では,式(a)は抗力の過小評価をし過ぎではないかと考えて,すこし工夫して,線形ぽく計算してみました(普通にやっても同じですが...);

辺々をv(t)で割って,変数分離を狙います;
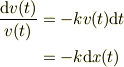
と無事に,辺々は全微分になるので,適当な初期条件のもと,

式(2)で,今度は,xとtとで変数分離して積分すると;
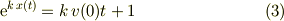
上記の2つの式を合わせれば,
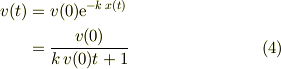
ちなみに,式(b)の場合では,

ですね.式(4),(5)をより比較しやすくする為に,式(4)の定数 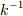 は長さのディメンションであることに着目して,
は長さのディメンションであることに着目して,

とすると,
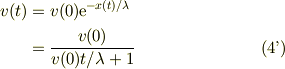
となります.
少なくとも,水泳では,両者の挙動は「だらだらした運動」としては大差がないなあ,と思いました.
勿論,抗力を明確な理論式で誘導する時には,その式の物理的な意味を保持する上で,正確な計算が必要でしょう.
でも,今回のように,「実験値の振る舞いを空気抵抗を取り入得るとどうだろうか?」といった直裁な質問では,あまり違いが無かろうと感じました.
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 【追伸:2007-11-11 ~02:00】
抗力が二次の場合の進行距離について
式(3)の自然対数を採れば直ちに,
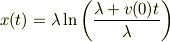
漸近値をもたないですね.