電磁波の一般解

電磁波の一般解

まぴお さんの書込 (2007/11/06(Tue) 19:28)

再び質問にやってきてしまいました． 以前，Mie散乱などについて質問したものです．

今回の疑問は，電磁波に関する波動方程式を極座標で解く際， TE 波(transverse electric wave)とTM波(transverse electric wave）の 線形結合で一般解が表される

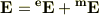
\bf{E}= {}^e\bf{E}+{}^m\bf{E}
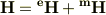
\bf{H}= {}^e\bf{H}+{}^m\bf{H}

という内容についてです．TEとTM波が互いに線形独立であることは， 知識としてなんとなくは知っていましたが，いざこの問題に直面すると， z方向の磁場がゼロであるTM波とz方向の電場がゼロであるTE波のみで， なぜすべての電磁波を表すことができるのしっくりきません． 相変わらず電磁気学を不勉強なせいなのか，あるいは考えすぎなのか， 考えれば考えるほどどんどん深みにはまっていっているように感じてます． 何かヒントだけでも結構ですので，コメントをよろしくお願いいたします．

Re: 電磁波の一般解

toorisugari no Hiro さんのレス (2007/11/06(Tue) 21:34)

> z方向の磁場がゼロであるTM波とz方向の電場がゼロであるTE波

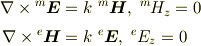
\nabla\times{}^{m}\bm{E} &=k~ {}^{m}\bm{H},~ {}^{m}H_z=0\\\nabla\times{}^{e}\bm{H} &=k~ {}^{e}\bm{E},~ {}^{e}E_z=0

ということですか?(理論をfollowしてないので，式に間違いがあったら訂正してください．)

それなら 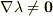\nabla\lambda\ne\bm{0} となる \lambda に対して

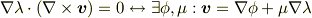
\nabla\lambda\cdot(\nabla\times\bm{v})=0 \leftrightarrow \exists \phi, \mu : \bm{v}= \nabla \phi + \mu \nabla\lambda

が成り立つことより 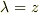\lambda=z とおいて，

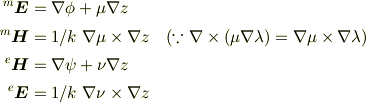
{}^{m}\bm{E}&=\nabla \phi + \mu \nabla z\\{}^{m}\bm{H}&=1/k~ \nabla \mu \times \nabla z \quad(\because \nabla\times(\mu\nabla\lambda)=\nabla\mu\times\nabla\lambda)\\{}^{e}\bm{H}&=\nabla \psi + \nu \nabla z\\{}^{e}\bm{E}&=1/k~ \nabla \nu \times \nabla z

が得られるので

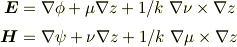
\bm{E} &=\nabla \phi + \mu \nabla z + 1/k~ \nabla \nu \times \nabla z\\\bm{H} &=\nabla \psi + \nu \nabla z + 1/k~ \nabla \mu \times \nabla z

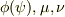となり，それぞれ， \phi(\psi),\mu,\nu の3個のパラメーター関数で表示されるので，「すべての電磁波を表」せそうです．

# きちんと証明しないといけないですが．．．

Re: 電磁波の一般解

まぴお さんのレス (2007/11/07(Wed) 12:30)

返答，ありがとうございました． まだ証明できてませんが，頑張ってやってみたいと思います．

Re: 電磁波の一般解

toorisugari no Hiro さんのレス (2007/11/07(Wed) 14:59)

> まだ証明できてませんが，頑張ってやってみたいと思います．

導出の証明?「すべての電磁波を表」すことの証明? 後者なら

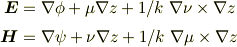
\bm{E} &=\nabla \phi + \mu \nabla z + 1/k~ \nabla \nu \times \nabla z\\ \bm{H} &=\nabla \psi + \nu \nabla z + 1/k~ \nabla \mu \times \nabla z

の各項が一次独立であることをしめせば十分なのでは? つまりスカラー三重積

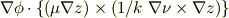
\nabla \phi\cdot\left\{ (\mu \nabla z) \times (1/k~ \nabla \nu \times \nabla z)\right\}

が0でないこと(or 0でない条件が与えられた条件に含まれること)を示せばよいのでは?

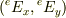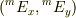追伸(11/8) : ({}^eE_x,{}^eE_y) と ({}^mE_x,{}^mE_y) が平行でないなら良いようです．物理的状況がわからないので，これ以上はコメントできません．

前者ならベクトル解析を勉強してください．