極座標のラプラシアンを微分形式で
極座標のラプラシアンを微分形式で
SDS さんの書込 (2007/11/05(Mon) 02:31)
極座標のラプラシアンを微分形式で求める方法が今ひとつ分かりません. あるいは,もっと一般化して,一般化座標の微分演算子でもよいです. (なお,授業等で出された課題ではなく,独学していて疑問を生じた点です)
物理系の大学2年生で,ある程度のベクトル解析の知識はあります. (微分形式を使わずに,力ずくでなら極座標のラプラシアンも求められます) 多様体に関してはノータッチ, テンソル解析に関しては特殊相対論や初歩の連続体力学で用いる程度の知識のみです. 微分形式に関してはベクトル解析の講義で, 外微分の定義とヤコビアンを用いた座標変換,一般のストークスの定理について軽く触れた程度です. ほとんどは当サイトのJohさんの文章で独学していますが,正しく理解できていない可能性も高いです.
を読んだのですが,

と,正規直交基底を持ち出してくれば何となく上手くいくような気はしますが,
そうする意味や必然性が分かりません.
また,今回は極座標ですから 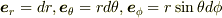 となるのも感覚的に理解できますが,
一般の座標変換だとこれをどのように求めればよいのでしょうか.
どことなく騙されたような気分です^^;
となるのも感覚的に理解できますが,
一般の座標変換だとこれをどのように求めればよいのでしょうか.
どことなく騙されたような気分です^^;
教えていただければ嬉しく思います.
Re: 極座標のラプラシアンを微分形式で
toorisugari no Hiro さんのレス (2007/11/05(Mon) 14:06)
> 極座標のラプラシアンを微分形式で求める方法が今ひとつ分かりません. > 力ずくでなら極座標のラプラシアンも求められます > 物理系の大学2年生で,ある程度のベクトル解析の知識はあります.
すごいですね.でも,いきなり,微分形式やテンソルにいく前にやることはあると思います.
# 力業とは変数変換に基づく成分計算ですよね.
では,問題を出しましょう.
「極座標系における勾配の式,微小体積要素の式はわかっている.これと 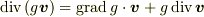 ,
, 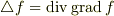 およびガウスの定理
およびガウスの定理
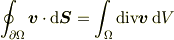
「のみ」を使って極座標のラプラシアンの式を導け.なお,場は2回偏微分可能で,無限遠方では速やかに0に近づくとしてよい(関数の一価性も仮定してよい).」 これが自力でできないのなら,微分形式におけるラプラシアンに手を出すのは早いです.:-)
Re: 極座標のラプラシアンを微分形式で
toorisugari no Hiro さんのレス (2007/11/06(Tue) 17:48)
一日待って返事がないということは,あきらめられたか,微分形式と関係ないと思われたかなのでしょうね.
半分だけやってみましょうか.じつはほとんどGreenの定理の証明です.
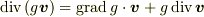 の両辺を全空間で体積積分すると
の両辺を全空間で体積積分すると
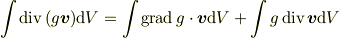
となります. 左辺はガウスの定理より
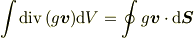
ですが,「無限遠方では速やかに0に近づく」という条件により右辺は0になります.つまり,
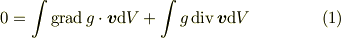
という式がでます.
これに, 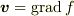 を代入すると,
を代入すると,
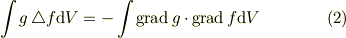
という式が得られます.
実はこれが微分形式におけるラプラシアンの定義式 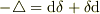 と本質的に同じものなのです.
と本質的に同じものなのです.
(2)の式は積分と内積が入っていて,微分形式と違うように見えますが,「Hodge *-双対」や「余微分作用素」といった概念をつかって(2)の式を翻訳し(一般化し)てるにすぎません. # 本当はベクトル場に作用するラプラシアンに対しても(2)と同様の関係式を求めなければいけないのですが...
つまり,「極座標のラプラシアンを微分形式で求める方法」は本質的には(2)を使って極座標のラプラシアンを求める方法なのです.特に自然基底でなく,正規直交基底で計算するのなら,微分形式よりこの方法が適しています.
どう求めるか,極座標系に限定せず,一般の曲線「直交」座標系 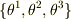 でやりましょう(右手系とします).
位置ベクトル,接ベクトルは
でやりましょう(右手系とします).
位置ベクトル,接ベクトルは
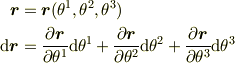
なので, 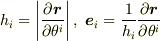 とおけば,
とおけば, 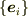 は正規直交基底になります.これより,
は正規直交基底になります.これより,
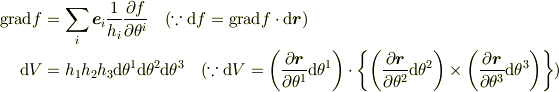
です.ちなみに極座標系 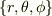 では
では 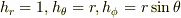 です.
以上を(2)の右辺に代入して
です.
以上を(2)の右辺に代入して
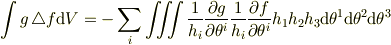
あとは,これを「部分積分」するだけです.「力ずくの計算」に比べて,遙かに簡単にできます.
なお, ![\int gf'\mathrm{d}x = [gf] - \int g'f\mathrm{d}x](http://hooktail.maxwell.jp/bbslog/fbfc2f3e58ac464d89beea8e71e61030.png) の右辺第一項に当たる部分は,表面積分が無限遠方で0という条件で消えたように,無視すればよいです.(まじめにやるといろいろ難しいことがありますが...)
の右辺第一項に当たる部分は,表面積分が無限遠方で0という条件で消えたように,無視すればよいです.(まじめにやるといろいろ難しいことがありますが...)
Re: 極座標のラプラシアンを微分形式で
SDS さんのレス (2007/11/07(Wed) 01:34)
すいません,返信せずに^^; 関係ないと思ったわけでもあきらめたわけでもなく,単に行き詰まっていました. 何をしていたかというと,
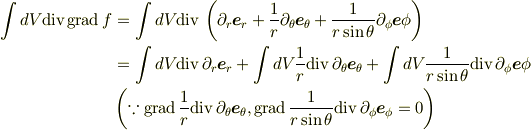
という一見それらしい式変形を行って, あとはガウスの定理を使ってどうやって極座標の基底の発散を表すかという, 実に見当外れの方向で悩んでいたわけですが^^;
とりあえず,提示してくださった方向に従ってやってみます.
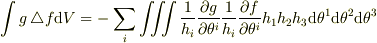 の右辺を極座標に即して書き直すと,
の右辺を極座標に即して書き直すと,
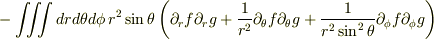 ところが
ところが
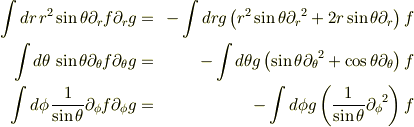
を踏まえて整理すると,(とりあえず部分積分が消えるのを認めれば)右辺は
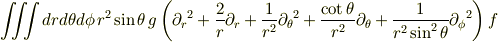
となり,被積分関数が等しいとして良い(?積分範囲を全空間に飛ばしたときだけ「偶然」等しくなるような気もしますが)とすれば,
 ということでよろしいでしょうか?
ということでよろしいでしょうか?
Re: 極座標のラプラシアンを微分形式で
toorisugari no Hiro さんのレス (2007/11/07(Wed) 15:29)
まだ続けられますね.よかった. 部分積分をやりましょう
![\int g\,\triangle f \mathrm{d}V &= -\int \mathrm{grad} g \cdot \mathrm{grad} f \mathrm{d}V\\&= -\sum_i \iiint \frac{1}{h_i}\frac{\partial g}{\partial \theta^i} \frac{1}{h_i}\frac{\partial f}{\partial \theta^i} h_1 h_2 h_3 \mathrm{d}\theta^1\mathrm{d}\theta^2\mathrm{d}\theta^3\\&= -\sum_i \iiint \frac{\partial g}{\partial \theta^i}\left(\frac{h_1 h_2 h_3}{h_i^2}\frac{\partial f}{\partial \theta^i}\right)\mathrm{d}\theta^1\mathrm{d}\theta^2\mathrm{d}\theta^3\\&= -\sum_i \left[\iint g \frac{h_1 h_2 h_3}{h_i^2}\frac{\partial f}{\partial \theta^i}\mathrm{d}\theta^1\mathrm{d}\theta^2\mathrm{d}\theta^3/\mathrm{d}\theta^i\right]_{\theta_i}\\&+ \iiint g \sum_i \frac{\partial}{\partial \theta^i} \left(\frac{h_1 h_2 h_3}{h_i^2}\frac{\partial f}{\partial \theta^i}\right)\mathrm{d}\theta^1\mathrm{d}\theta^2\mathrm{d}\theta^3\\&= \iiint g \sum_i \frac{1}{h_1 h_2 h_3}\frac{\partial}{\partial \theta^i} \left(\frac{h_1 h_2 h_3}{h_i^2}\frac{\partial f}{\partial \theta^i}\right)h_1 h_2 h_3 \mathrm{d}\theta^1\mathrm{d}\theta^2\mathrm{d}\theta^3\\&= \int g \sum_i \frac{1}{h_1 h_2 h_3}\frac{\partial}{\partial \theta^i} \left(\frac{h_1 h_2 h_3}{h_i^2}\frac{\partial f}{\partial \theta^i}\right)\mathrm{d}V](http://hooktail.maxwell.jp/bbslog/429e89f67015d7f360822b8e1df1cade.png)
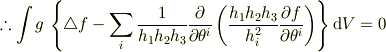
ここで「任意の関数 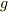 で
で 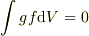 なら
なら 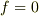 」より
」より
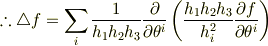
が得られます.
極座標系では 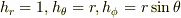 より,
より,
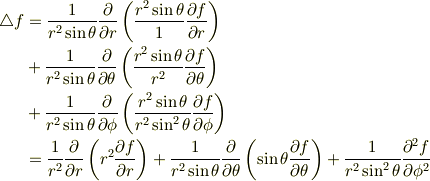
が得られます.さらに変形すると
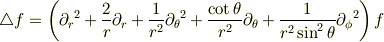
になるはずです. 計算量としては変わらないかもしれませんが,計算手順がはっきりわかっている分,体当たりより楽ですね.この手順を抽象化し,操作主義的にまとめたものが微分形式のラプラシアンです.自然基底を学ぶまでは,とりあえず,正規直交基底と積分と内積を使うこの計算法にとどめて置いた方が良いと思います.
# 余力があるなら,練習問題として,先の(1)から  の極座標表示を導いてみてください.
の極座標表示を導いてみてください.