面積分の計算と概念について
面積分の計算と概念について
えり さんの書込 (2007/10/31(Wed) 22:08)
お久しぶりです. 今,面積分の計算の仕方でつまずいています.教科書で面積分の解説を読むと,いいたいことはなんとなくわかるのですが,実際に解くとなるとどこから手をつけていいのかわかりません.おそらく概念もあやふやなのだろうと思います.(過去ログも検索致しましたが,あまり理解できませんでした…)
例えば,
半径  の球面
の球面  で,次の面積分を計算せよ.
で,次の面積分を計算せよ.
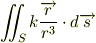
ただし, 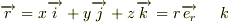 は定数
は定数
といった問題があったときに,まずこの被積分関数がどういうことを表していることもわからないし, 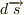 をどう計算に組み込ませればいいのかもわかりません.すごく基本的な質問で恐縮ですが,どなたかご教授していただけないでしょうか.よろしくお願いいたします.
をどう計算に組み込ませればいいのかもわかりません.すごく基本的な質問で恐縮ですが,どなたかご教授していただけないでしょうか.よろしくお願いいたします.
Re: 面積分の計算と概念について
tip★ さんのレス (2007/10/31(Wed) 23:02)
インテグラルの数は1つにしたほうが良いかと・・・自分も前指摘されました.
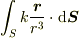
自分は,解析学とかの講義で実際面積分を習ったことはありませんが,電磁気学でちょちょっと習いました.他の人の意見も聞いてください.
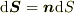 だたし,
だたし, 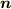 は閉曲面Sの法線ベクトル
は閉曲面Sの法線ベクトル
としたら分かりませんか?
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/01(Thu) 11:50)
えりさん # 長いです.注意してください.
> 半径Rの球面Sで,次の面積分を計算せよ. > |ed92cd3ea50d1588b27dfc90faaf247c| ただし, |0baf60cd0f57e2004899e052992e066b| は定数 ::
> といった問題があったときに,まずこの被積分関数がどういうことを表していることもわからないし, 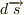 をどう計算に組み込ませればいいのかもわかりません.
をどう計算に組み込ませればいいのかもわかりません.
まず,面積分を語る前に積分に付いて語ります.
積分にはふたつの目的があります. (1) 幾何学的,物理的な事象の一般的関係を「記述」すること (2) 個別の事象に対して具体的に量を「計算」すること
もちろん,(2)は大事なのですが,大学ではどちらかというと第2義的なものになります.一番大事なのは,本質的なのは(1)です.
大学の講義では物理の支配方程式を導くこと,及び,定性的な性質を導くことが,すなわち「記述」が目的です.個別の事例の具体的な定量「計算」をすることもありますが,あくまでもそのあとです.
ベクトルでも, (1)成分表示せずに『ベクトル』で式を「記述」し,内積,外積,微分,積分などの一般的な処理をする. (2)必要ならば,座標系(および計量)を指定して,具体的な成分「計算」をして値をだす. という処理をするはずですが,積分でもおなじです.
これを理解しないで積分とは「計算」なのだという意識で大学の講義を受けると「何を言いたいのかわからない」状態になりかねません.
面積分が質問ですが,面積ベクトルやら積分の中のベクトル演算を説明するのは大変なので,以下の「簡単」な問題から考えましょう.(これが理解できたら面積分に移りましょう.)
「(問題1) ある連続体中にとられた領域 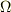 の質量
の質量 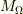 を求めよ.ただし,位置
を求めよ.ただし,位置  における密度は
における密度は 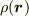 で与えられているとする.」
で与えられているとする.」
この問題,どう解きます?
「えっと,  座標は...範囲は...いやいや,領域の体積×密度は...」とやっていたらとけませんよね.
座標は...範囲は...いやいや,領域の体積×密度は...」とやっていたらとけませんよね.
で,どう,解くか.少し冗長な記述をさせてください.
この問題を解くのに必要な概念は (a) 全体の質量は個別の質量の和である.(足していく順番=座標系に依存しない) (b) 質量分布が一様な領域では「質量=密度×体積」である. (c) 十分に微小な領域を考えると,関数は線形(あるいは一定)と見なせる. です. # (c)は微積分の基本哲学ですね.
これに従って解いていきましょう.
(1). 位置  を含む微小な領域を考え,その微小領域(
を含む微小な領域を考え,その微小領域(  点
点  )の質量を
)の質量を 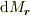 とおく.(a)より
とおく.(a)より
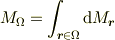
(2). 微小な領域では,(c)より質量分布が一様(密度一定)と思って良いので,1.の微小領域の体積を 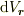 と置くと,(b)より微小領域(
と置くと,(b)より微小領域(  点
点  )の質量は
)の質量は
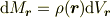
と書ける. (3). 1.,2.より
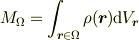
これで,完成です.え,これじゃ計算できないと思うかもしれませんが,必要ありません.「記述」を問う問題だからです. 計算は,次の問題がでたらやればいいのです.
「(問題2) 一つの頂点を原点におき, 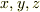 各座標軸に辺が乗っている,一辺が
各座標軸に辺が乗っている,一辺が  の立方体の質量を求めよ.ただし,位置
の立方体の質量を求めよ.ただし,位置 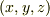 における密度は
における密度は 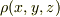 で与えられているとする.
」
で与えられているとする.
」
問題1と問題2の大きな違い,わかります?2には座標系(デカルト座標系)が設定されています.座標系が設定されて,初めて多重積分や1次元積分に直せます.でも,抽象的な一般論には座標系は必要ないのです.
さあ,解きましょう.
(4). デカルト座標系では,位置 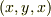 を含む
を含む 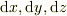 の微小領域の体積は
の微小領域の体積は 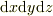 である.
(5). 問題1より質量
である.
(5). 問題1より質量 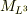 は
は
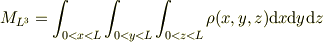
終了です.さらに 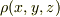 の具体的な関数形を与え,具体的な質量を問う問題3(ex.「
の具体的な関数形を与え,具体的な質量を問う問題3(ex.「 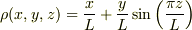 のとき質量は?」)があれば,高校でやるような「積分計算」((6).
のとき質量は?」)があれば,高校でやるような「積分計算」((6).
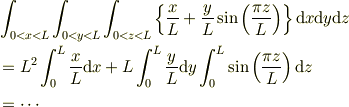
)の世界が待っています.
以上のように積分の問題は I. (座標系によらない)幾何学的な性質を記述する.(逆に記述から物理的性質を読み解くこともあります.) (I'. ガウスの定理の様に幾何学的定理を使って,別の積分に変換する.) II. 座標系を設定し,多重積分に書き換える.(さらに,系に対称性があれば,1次元積分などに書き換える.) III. 具体的な関数形に従って積分計算を行う. という手順で解きます.問題によってはこれらが混在したものもありますが,解く側が頭の中でoutlineを上の三つの処理に分解して考えなければいけません.
非常に冗長になってしまったので,わかってもらえないと思いますが,質問も交え,ゆっくり,語っていきましょう.
# tip★さん.積分の表記,完璧です.(特に 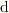 ).これが,偏微分の表記で喧嘩した:-)方とは思えません.ずいぶん,勉強されましたね.
).これが,偏微分の表記で喧嘩した:-)方とは思えません.ずいぶん,勉強されましたね.
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/02(Fri) 00:22)
えりさんに質問です.
> まずこの被積分関数がどういうことを表していることもわからないし,
面積ベクトルとは何か,わかりますか?あるいは,以下の問題が解けますか?
「速度 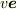 (
(  は単位ベクトル,
は単位ベクトル, 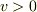 )で水が一様に流れている.ある閉曲線で囲まれた面積
)で水が一様に流れている.ある閉曲線で囲まれた面積  の仮想「断面」を時間
の仮想「断面」を時間 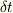 に(裏から表に)通過する水の体積を求めよ.ただし,断面の単位法線ベクトルは
に(裏から表に)通過する水の体積を求めよ.ただし,断面の単位法線ベクトルは 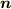 で面の裏から表への向きである.」
で面の裏から表への向きである.」
(これがわからないなら,「また,  と
と 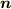 のなす角を
のなす角を  とする.」という文を追加します.)
とする.」という文を追加します.)
「半径  の球面
の球面 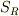 上の微小面積要素の面積を
上の微小面積要素の面積を 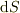 ,面の単位法線ベクトル(球の外側を向いている)を
,面の単位法線ベクトル(球の外側を向いている)を 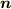 と表す.球面全体におけるすべての微小面積要素に対して定義された積分
と表す.球面全体におけるすべての微小面積要素に対して定義された積分
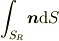
の値はいくらか?」
Re: 面積分の計算と概念について
zoro さんのレス (2007/11/02(Fri) 01:04)
TeX使いになってカムバックされて,おめでとうございます.
ご質問の数学的な解釈は,皆さんに任せるとして,イメージの事を書いてみたいと思います.
恐らく,電磁気でも,ガウスの発散公式;ヴェクタ場の面積分が,その場の発散の体積分に等しいというのを見て,大変に驚いた事を今でもはっきりと覚えています(笑).
で,ヴェクタ場の面積分をどう考えるか,悩んだものです.うろ覚えですが,当時の感じを書いてみます.
ある場の量として,太陽から流れる光のエネルギ流量が,位置の関数であらわせて, 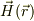 だとします.そして,位置,
だとします.そして,位置, 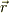 小さな微小面積,
小さな微小面積, 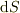 が単位ヴェクタ,
が単位ヴェクタ, 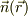 の方向に内側から外を向いているとします.
の方向に内側から外を向いているとします.
このとき,微小面を中側から外側に流れる微小流量, 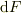 は,
は,
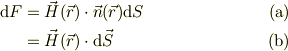
ここで微小面積ヴェクタは;

です.式(c)を仲介に,式(a)から出発しても,式(b)からでも,都合の良いほうから考えれば良いですね.
当時,陽射しの強い日に,均一な平行光線だから, 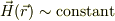 として,掌の暖かさを,角度を変えて実感したものです.
として,掌の暖かさを,角度を変えて実感したものです.
後は,ヴェクタ場なら,流量だけでなく,力でも良い訳で....
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/02(Fri) 01:13)
ダメでしょう,zoroさん,先に答えを書いちゃ:-)
でも
> 当時,陽射しの強い日に,均一な平行光線だから, 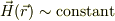 として,掌の暖かさを,角度を変えて実感したものです.
として,掌の暖かさを,角度を変えて実感したものです.
というのは感覚的にわかるよい演示法ですね.
Re: 面積分の計算と概念について
tip★ さんのレス (2007/11/02(Fri) 01:28)
私が電磁気学で線積分や面積分を習ったとき最初悩んだ事を書いてみようと思います.
「内積とは何を意味するか.特に,単位ベクトルとの内積は何を意味するのか?」
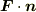 ただし,
ただし, 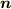 は単位ベクトルとする.
は単位ベクトルとする.
この計算は, 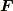 の大きさを
の大きさを  ,
, 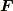 と単位ベクトル
と単位ベクトル 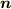 のなす角を
のなす角を  とすると,
とすると,
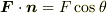
となります.
私の解釈では,単位ベクトルとの積分の意味は「 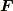 の単位ベクトル成分のみを取り出す」ことだと思います.
の単位ベクトル成分のみを取り出す」ことだと思います.
どこで悩んでいるのかわかりませんが,一応書いておきます.
#toorisugari no Hiroさん,その時はどうもすみませんでした.確かに勉強は少ししましたが,本を手に取ると急にやる気が無くなってしまうことが多いです・・・,みなさんはどのようにして知識を蓄えているのでしょう?疑問です.
Re: 面積分の計算と概念について
zoro さんのレス (2007/11/02(Fri) 14:15)
昨晩は,朦朧として書いたので,中途半端な説明になっていました.少し補強します.
「ヴェクタ場」と言う言葉にこだわったのは,学生のころ,「水流」みたいな概念で,延々と説明を受けた後,急に「電場」の話になって違和感を強くもったので,場所毎に決まるヴェクタとしての場と書きました.
わけても,場所に依らずに「一定の方向と大きさ」を持つ「一様なヴェクタ場」を基に感覚を養っておくのは,大雑把な問題把握に役立つと思います.その例を挙げると;
・日常的なスケールでの地球の「重力場」. ・安定した水量と幅をもつ川の「流れの場」,ミシシッピ川. ・面積の大きな平行版コンデンサがつくる「電場」. ・光源から遠く離れた処での「光のエネルギ流」や「電場・磁場」. ・大きな駅で階段を通過する「多体系としてのヒトビトの通行流」.
などがあると思います.もっと良い例があれば,皆さんもお知恵をお教え下さい.
さて,ある一様な場の量, 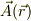 が,座標系Oxyzの中で,x軸を向いて流れているとします.
が,座標系Oxyzの中で,x軸を向いて流れているとします.
#電場や重力も流れていると思っておくと,イメージし易いかもしれません.
そこで,流れに対して,掌の替わりに「かまぼこの台」を試験片としていれます.この長辺の長さを, 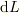 ,短辺の長さを,
,短辺の長さを, 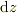 ,とし,短辺がz軸に並行に,長辺がxy平面に並行であるとします.
,とし,短辺がz軸に並行に,長辺がxy平面に並行であるとします.
<pre>
y軸
↑(試験片の表側)
|長辺:dL
|∠R 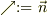 |/
|(試験片の裏側)∠θ
| ーー→
|/
|(試験片の裏側)∠θ
| ーー→ 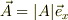 |
|
+ーーーーーーーーーーーーーーーーーーー→ x軸
</pre>
|
|
+ーーーーーーーーーーーーーーーーーーー→ x軸
</pre>
試験片の向きは,単位法線ヴェクタ, 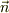 であるとします.従って,その微小面積ヴェクタは;
であるとします.従って,その微小面積ヴェクタは;
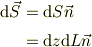
と定義するとします.此処で,場のヴェクタの方向 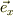 と試験片の単位法線ヴェクタとの成す角を,
と試験片の単位法線ヴェクタとの成す角を,  とします.
とします.
さて,本題ですが,ヴェクタ場が微小面積片に流出する量, 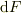 を典型的な角度
を典型的な角度  から考えます.
から考えます.
なお,以下では,ある一定の地点に微小面積片を置き,その微小面積片がヴェクタ場となす角度ごとに,場の流入出を考える事にします.
●Case1 ヴェクタ場の流れが面の内側から垂直に出ていく時:∠θ=0●
流出量は,幾何学的な面積に,場の強さを掛ければ良いのですから,素直に;

●Case2 ヴェクタ場の流れが面と平行な時:∠θ=π/2●
流れが,面に平行なら「出るのも,入るのも無い」ので,

●Case3 ヴェクタ場の流れが面と対抗している時:∠θ=π●
ヴェクタの流れが,面の外側から垂直に入射するので,流入すなわち流出の逆符号状態,「Case1」の逆符号状態,となりますね.

●Case4 ヴェクタ場の流れが面からθの角度で流出している時●●
dLの要素を通過する場の流れは,明らかにdL'の要素を通過するのだから,
<pre>
y軸
↑
|長辺:dLdL' = dL*cos(θ)
|∠θ | 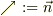 ||/
|| / ∠θ
| |/ ーー→
||/
|| / ∠θ
| |/ ーー→ 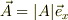 |
|
+ーーーーーーーーーーー→ x軸
</pre>
|
|
+ーーーーーーーーーーー→ x軸
</pre>
仮想的に,dL'の微小面積素について,「Case 1」の計算をすれば良いのだから,
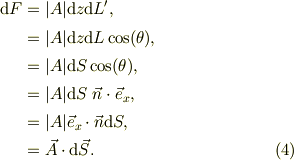
と考えて善いのだと,思います.
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/02(Fri) 17:27)
> 「内積とは何を意味するか.特に,単位ベクトルとの内積は何を意味するのか?」
これは難しい問題です.かえって「外積」の方が面積というイメージがあるので簡単かもしれません.
ベクトルとの内積といっても,それが直線に平行な接ベクトルか平面に垂直な法線ベクトルか,極性ベクトルか軸性ベクトルか,,,で,幾何学的なイメージが異なってきます.(というか幾何学的に異なる4種類(8種類?)のベクトルがあるのに,それを同一と見なしてるあたりに問題があるんですが.)
ただ,積分でよく使う2種類の内積
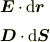
のイメージをおさえておけば,まずは何とかなります.(通常の「射影」を表す内積とは別物です.上のふたつは内積というより縮約というべきかもしれません.)
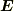 は電場に代表されるベクトル場です.静電場
は電場に代表されるベクトル場です.静電場
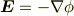
が典型です.イメージは等高線(等値面),つまり,曲面の層です.
等高線を書けば,勾配ベクトルはすぐ計算できるので,このベクトル場は「矢印ベクトル」の集団でなく,高低つきの等高線(等値面)そのもので作図します.
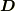 は電束密度に代表されるベクトル場です.電束密度は電気力線の束の(面)密度を大きさにもつ電気力線と平行なベクトルです.流線束や光線束や電荷の軌道線束(電流密度)を表現するベクトルもこの仲間です.イメージは曲線の束,あるいはチューブの集まりです.
向きのついた曲線束で作図します.
は電束密度に代表されるベクトル場です.電束密度は電気力線の束の(面)密度を大きさにもつ電気力線と平行なベクトルです.流線束や光線束や電荷の軌道線束(電流密度)を表現するベクトルもこの仲間です.イメージは曲線の束,あるいはチューブの集まりです.
向きのついた曲線束で作図します.
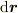 は微小矢印ベクトル(接ベクトル)
は微小矢印ベクトル(接ベクトル)
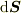 は微小面積ベクトル(法ベクトル)
です.このとき,
は微小面積ベクトル(法ベクトル)
です.このとき,
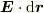 は曲面層の中に線分を置いたときの交点の数.
は曲面層の中に線分を置いたときの交点の数.
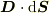 は曲線束の中に面分を置いたときの交点の数.
は曲線束の中に面分を置いたときの交点の数.
になります.(絵を描いて確かめてみてください.また,電位差や電束などの物理的な概念と矛盾しないことを確かめてください.) # 逆に交点の個数をこの組合わせの内積と定義してもいいくらいです.
このイメージがわかると面積分や線積分がわかりやすくなります.
# 上のふたつの「内積」は通常の内積とは異なると言いました.どちらかというと密度×体積に近い物です.
> みなさんはどのようにして知識を蓄えているのでしょう?疑問です.
知識は蓄えても使わなければ,単なる意味不明の「お経」です. 問題をがんがん解くしかないですね. すなわち,頭にではなく,手に蓄えましょう.
ここで,回答をするのが良い勉強になると思います.
> その時はどうもすみませんでした.
こちらこそ.
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/02(Fri) 19:42)
こんな問題を考えてみましょう.
問題0「光源から光が出ている.光源への直線と垂直となるように置いた面が受ける光量は,光源と面の距離  の何乗に比例するか?」
の何乗に比例するか?」
答えは「 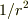 に比例する」ですね.
に比例する」ですね.
光量というのは面が受ける光線の本数に比例します.作図で,面を通る光線の本数は 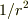 に比例することはわかりますよね.
# もちろん,本当は実験から「
に比例することはわかりますよね.
# もちろん,本当は実験から「 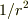 に比例する」がでて,それから「光量というのは面が受ける光線の本数に比例します」という考察がでるのですが...
に比例する」がでて,それから「光量というのは面が受ける光線の本数に比例します」という考察がでるのですが...
さて,前に説明した束ベクトルの考え方を導入しましょう.束の面密度に比例し,束を構成する直線に平行なベクトルです.光源を原点とすると束ベクトルは,単位動径ベクトル 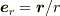 (
(  は面の位置ベクトル)に平行です.
は面の位置ベクトル)に平行です.
比例定数を  とすると,光線の束ベクトル(光量の面密度ベクトル)
とすると,光線の束ベクトル(光量の面密度ベクトル) 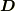 は
は
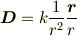
と表されます.(どこかで見ましたね.)
さて,位置  に,面積
に,面積 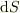 ,単位法線ベクトル
,単位法線ベクトル 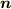 の微小面積要素があるとします.微小面積要素の面積ベクトルは
の微小面積要素があるとします.微小面積要素の面積ベクトルは 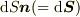 で表されます.
で表されます.
この面が受ける光量 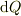 は?
は?
答えは 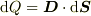 です.
です.
これって,前に密度の話をしたときの 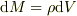 と似ていると思いませんか?それがみえたら,あとは,前と同じようにやればよいだけです.
と似ていると思いませんか?それがみえたら,あとは,前と同じようにやればよいだけです.
問題1 「光源を囲む閉曲面Sがうける光量はいくらか」 答え 「
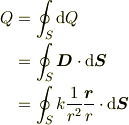
」
問題2 「閉曲面Sが光源を中心とする半径  の球面
の球面 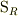 の場合,うける光量はいくらか」
の場合,うける光量はいくらか」
これは,次のフェーズ「座標系を設定し,多重積分にする.対称性があるときはそれを利用して積分を簡単にする」になります.
座標系は極座標系がよさそうですね.このとき
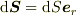 となることに気づけば,もう答えは見えました.
となることに気づけば,もう答えは見えました.
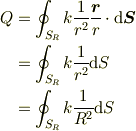
ここで,極座標系により多重積分に持ち込んで,積分計算をまじめにやってもいいのですが,簡単にやりましょう.被積分関数は定数です(回転対称性).ということは積分の外に出せてしまえます.
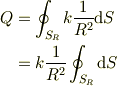
最後の積分は,球面の面積 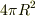 です.ということは,答えは
です.ということは,答えは
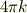
です.
余談
通常,曲面の形が決定されないと,積分計算はできません.つまり,問題2で初めて値が出るのです.しかし,この問題に限っては問題1の段階で,ある理論を使うと問題2と同じ 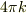 が出ます.
が出ます.
その理論がガウスの定理(ガウスの法則)です.
Re: 面積分の計算と概念について
tip★ さんのレス (2007/11/03(Sat) 21:31)
toorisugari no Hiroさんの内積の説明わかりやすくて,イメージしやすくなりました.ありがとうございます.
>>その理論がガウスの定理(ガウスの法則)です.
このように書くと,ガウスの定理とガウスの法則が全く同じ理論に見えてしまうような気がします.ガウスの定理は数学の理論で,ガウスの法則は電磁気学の理論ではないのですか?
Re: 面積分の計算と概念について
えり さんのレス (2007/11/03(Sat) 23:38)
返信遅れてすみませんでした. 実は連日忙しい日が続いておりまして,まだ,最後まで解説を読みきれていません. なので,この場を借りてまずはお礼を申し上げたいと思います.どうもありがとうございます.
また後ほど書き込みをさせていただきたいと思います.
Re: 面積分の計算と概念について
zoro さんのレス (2007/11/04(Sun) 07:48)
えりさん,
この掲示板は学校の講義と違って,疑問に思った事をとことん論議できる処だろうと思います.納得がいくまで,幾らでも質問されると良いと思います.
特に,ご質問が「ヴェクタ場」の持つ特質に絡む量,面積積分であり,微小領域の性質と,大局領域の性質との接点となる計算であると思います.それ故に,複数の人々が,自分の経験を基に説明しようと試みているのだろうと思います.
逆に言えば,とてもグッド・タイミングな質問なので,流されないように確りと関連質問をされる事をお勧めします.
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/05(Mon) 13:26)
> toorisugari no Hiroさんの内積の説明わかりやすくて,イメージしやすくなりました.ありがとうございます.
よかった.
>>その理論がガウスの定理(ガウスの法則)です.
> このように書くと,ガウスの定理とガウスの法則が全く同じ理論に見えてしまうような気がします.ガウスの定理は数学の理論で,ガウスの法則は電磁気学の理論ではないのですか?
もちろんそうです.ガウスの法則は「電束と電荷の間の経験則」です. そういう意味では「その理論がガウスの定理です.」というべきなんでしょうが...
でも,ガウスの法則は「束と端点の間の関係」つまり, 「閉曲面を通過する束の総数は,面で囲まれる領域内で発生(消滅)した線の個数(線の端点の個数)と等しい. 」 つまり,面を通過する(電気力)線の束の個数(電束)と(電気力)線の端点(始点,終点=荷電粒子)の個数(電荷)は等しいという幾何学的な「法則」ともみなせます.
そして単位体積あたりの線の端点の個数(個数密度)を「発散」と定義すれば
「束ベクトル 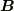 がある閉曲面
がある閉曲面 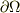 との間にできる交点の個数は,線の端点の個数密度
との間にできる交点の個数は,線の端点の個数密度 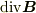 を閉曲面でかこまれる領域
を閉曲面でかこまれる領域 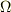 において体積積分したものに等しい.
において体積積分したものに等しい.
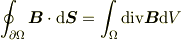
」
つまり,ガウスの定理になります. そして,直交座標系で「ガウスの定理」を計算することで
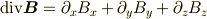
が導かれます.
要は,解析的な定義からガウスの定理にいくか,幾何学的な「法則」からガウスの定理にいくかの違いです.
Re: 面積分の計算と概念について
えり さんのレス (2007/11/06(Tue) 00:27)
長い間返信できなかったので,発言が間延びしてしまうと思いますが,お許しください.
まず,「面積分とは何か」という問いにはまだしっかりと答えられませんが,感覚はつかめました.足し合わさって面になるという考え方でいいのでしょうか.
tip★さんがご指摘して下さいましたインテグラルの数に関してですが,これは toorisugari no Hiroさんがおっしゃていた座標系の記述がないからでしょうか.逆に言えば,インテグラルが2つあるということは座標系での話をしているぞ,と思ってよいのでしょうか…?
それから, toorisugari no Hiroさんがご説明して下さった
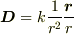 を見てはっとしました.同時に,「被積分関数が何を意味しているのか全くわからない」と前に発言した自分が恥ずかしかったです..
いかに私が物理量を無味乾燥的に記憶してしまっているのか,思い知らされ,反省しています.
を見てはっとしました.同時に,「被積分関数が何を意味しているのか全くわからない」と前に発言した自分が恥ずかしかったです..
いかに私が物理量を無味乾燥的に記憶してしまっているのか,思い知らされ,反省しています.
私は,法線ベクトルと内積をいつの間にか別個のものとして認識していたようです.zoroさんがご丁寧に図まで描いていただいたおかげで,
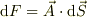 の意味が理解できました.
の意味が理解できました.
ただ, tip★さんが以前書き込みをして下さった, 「単位ベクトルとの積分の意味は「の単位ベクトル成分のみを取り出す」こと」というイメージがまだ湧きません…(すみません)
Re: 面積分の計算と概念について
tip★ さんのレス (2007/11/06(Tue) 02:43)
>>ただ, tip★さんが以前書き込みをして下さった, 「単位ベクトルとの積分の意味は「の単位ベクトル成分のみを取り出す」こと」というイメージがまだ湧きません…(すみません)
単位ベクトルとの積分ではなくて内積です.
自分の勝手な解釈なので,気にしなくても大丈夫ですよ.忘れてください. 内積の説明はtoorisugari no Hiroさんのを参考にしてください.
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/06(Tue) 11:03)
> まず,「面積分とは何か」という問いにはまだしっかりと答えられませんが,感覚はつかめました.足し合わさって面になるという考え方でいいのでしょうか.
そうですね.これが,リーマン積分の考え方です.
つまり,適当に面を分割して,面  を面素の集まり
を面素の集まり 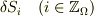 で考えればいいと言うことです.
で考えればいいと言うことです.
> tip★さんがご指摘して下さいましたインテグラルの数に関してですが,これは toorisugari no Hiroさんがおっしゃていた座標系の記述がないからでしょうか.逆に言えば,インテグラルが2つあるということは座標系での話をしているぞ,と思ってよいのでしょうか…?
私はそのように使っていますが,普遍的ではないです.面積分なら,座標系があろうがなかろうが 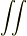 で表現する方もいます.が,上の
で表現する方もいます.が,上の 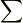 が2重の
が2重の  でないように積分も2重にする必要はないと思います.
でないように積分も2重にする必要はないと思います.
x,y座標系を採り,格子に分割したら
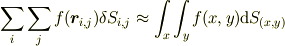
となりますが... # もちろん
とともできます...
> それから, toorisugari no Hiroさんがご説明して下さった |a3f5747e6a2296a623f6fb78d4c2090f| を見てはっとしました.同時に,「被積分関数が何を意味しているのか全くわからない」と前に発言した自分が恥ずかしかったです..
ま,初学者では珍しくないので,あまり恥じ入る必要はないです.読むこと,書くことは結構難しく,かつ,重要なことなんだと理解してもらえばいいです.
大学では,計算することより,記述すること,記述から意味をくみ取ることが重要になります(それがすべてといってもいい).がんばってください.
Re: 面積分の計算と概念について
toorisugari no Hiro さんのレス (2007/11/06(Tue) 11:41)
> 私の解釈では,単位ベクトルとの内積の意味は「 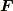 の単位ベクトル成分のみを取り出す」ことだと思います.(修正しました)
> 自分の勝手な解釈なので,気にしなくても大丈夫ですよ.忘れてください.
の単位ベクトル成分のみを取り出す」ことだと思います.(修正しました)
> 自分の勝手な解釈なので,気にしなくても大丈夫ですよ.忘れてください.
射影という意味ならまちがいでないです.ともに同じ空間に属するベクトルの場合,内積は射影となります.(どれだけそろっているか(平行)を表す「相関」ですね.)
内積が与えられたら,大きさや角度が計算できます.この意味でともに同じ空間に属する(同種の幾何学的対象の)ベクトルの内積を「計量」と呼びます.
計量と縮約は内積としての代数操作は同じですが,意味は違います.
Re: 面積分の計算と概念について
えり さんのレス (2007/11/06(Tue) 15:18)
toorisugari no Hiroさん 「読むこと,書くことは結構難しく,かつ,重要なことなんだと理解してもらえばいいです.大学では,計算することより,記述すること,記述から意味をくみ取ることが重要になります」 はい,しっかりと意識して大学で勉強していこうと思います.
二重積分のことも納得できました.時と場合によって使い分けられるようにしたいと思います.
みなさん,本当にどうもありがとうございました.