2変数関数の極大と極小
2変数関数の極大と極小
リッチ さんの書込 (2007/10/31(Wed) 04:30)
こんばんは.リッチです.
問題関数f(x,y)=(1/3)x^3-x^2y+xy^2-y^2-x+yについて極大と極小を求めたい.次の手順で求めよ. (1)2階の偏導関数f_xx,f_xy=f_yx,f_yyをそれぞれ求めよ. (2)Hessian H(f)の符号を求めることにより,極値の候補がそれぞれ極大・極小・鞍点のどれであるか判別せよ.
- f_xx=2x-2y, f_xy=f_yx=-2x+2y, f_yy=2x-2
(2)極値の候補はf_x=f_y=0より,(x,y)=(1,0)(-1,0)(1,2)(3,2)となる. (1,0)のとき,H(f)=4でf_xx>0だから極小 (-1,0)のとき,H(f)=4でf_xx<0だから極大 (1,2)のとき,H(f)=-4だから鞍点 (3,2)のとき,H(f)=12でf_xx>0だから極小
上記のようになったのですが,合っていますでしょうか? 最近ことごとく計算ミスに悩まされています.よろしくお願いいたします.
Re: 2変数関数の極大と極小
スパイク さんのレス (2007/11/04(Sun) 16:48)
こんにちは.
ヘッセの行列の対角成分と対称性を見ればいいと思います.
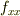 ,
, 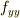 が
が  の時と,
ヘッセの行列式(
の時と,
ヘッセの行列式( 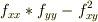 )が,正負を取るときは?
)が,正負を取るときは?
#意味が判ればいいのではないでしょうか.