スカラーポテンシャルによる場の表示
スカラーポテンシャルによる場の表示
まぴお さんの書込 (2007/10/30(Tue) 21:03)
現在,球体による電磁波の散乱(いわゆるMie理論)を勉強しています.それに関連して,以前波動方程式について 質問させていただきましたが,あらたにわからないところがあったので再び投稿させていただきます. Maxell方程式より
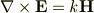
と与えられ,これをさらに極座標で表すと
になるかと思います(ただし動径成分しか示していません).
ここでTE波を考えると, 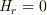 なので,(1)式より
なので,(1)式より
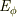 および
および 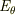 はスカラー関数の勾配
はスカラー関数の勾配
によって表現できる(と,手元のテキストには書いてあります.ちなみにテキストはMax Born著の「光学の原理」です).そこで
と置くと,式(2)は
になる(と,これもテキストに書いてあります).まず,偏微分にあまり慣れていないせいかもしれませんが,
(1)式から(2)式がどうやって得られるのかわかりません(質問1).加えて,式(2)でいきなり  が出てきたかと思ったら,
式(3)では
が出てきたかと思ったら,
式(3)では 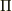 (テキストによる,Debyeポテンシャルと呼ばれるスカラーポテンシャルに相当すると書かれています)で
置き換えられていて,物理的意味があるのか,あるいは単に数学的に計算しやすくするために導入したのか,
よく理解できません.長くなって申し訳ありませんが,教えていただけませんか.よろしくお願いいたします.
(テキストによる,Debyeポテンシャルと呼ばれるスカラーポテンシャルに相当すると書かれています)で
置き換えられていて,物理的意味があるのか,あるいは単に数学的に計算しやすくするために導入したのか,
よく理解できません.長くなって申し訳ありませんが,教えていただけませんか.よろしくお願いいたします.
Re: スカラーポテンシャルによる場の表示
まぴお さんのレス (2007/10/30(Tue) 21:40)
すみません.間違えていましたので,訂正しました.
Re: スカラーポテンシャルによる場の表示
toorisugari no Hiro さんのレス (2007/10/30(Tue) 22:08)
> (1)式から(2)式がどうやって得られるのかわかりません(質問1).
Bornの論法や計算がわからないので,くわしいことは不明ですが,
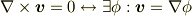
というベクトル解析の基本定理を使ってスカラポテンシャルを求める論法ではないのですか?
(3)以下はわかりません.
Re: スカラーポテンシャルによる場の表示
yama さんのレス (2007/10/31(Wed) 00:05)
基本的には toorisugari no Hiro さんが書かれたような考え方でいいと思いますが,問題はベクトルの回転自体は0でなく,回転のr成分だけが0の場合はどうなるかということですね.
簡単のためデカルト座標で考えて, 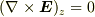 すなわち
すなわち 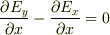 が成り立てば
が成り立てば
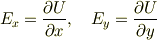
となるようなスカラーポテンシャルU(x,y,z)が存在することは容易に分かります. すなわち,ある方向の回転の成分が0であれば,それに垂直な面内のベクトル成分はスカラーポテンシャルの勾配で表すことができるということです.
極座標の場合も同様で,回転のr成分が0であればそれに垂直なθ成分とφ成分はスカラーポテンシャルの勾配で表されると言えるでしょう.
Re: スカラーポテンシャルによる場の表示
まぴお さんのレス (2007/10/31(Wed) 10:06)
toorisugari no Hiro さん,yamaさん,ありがとうございました.なんとなくわかったような気がします.
yamaさんに確認ですが,
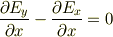
は
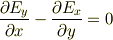
ですか?間違えていたらすみません.
Re: スカラーポテンシャルによる場の表示
yama さんのレス (2007/10/31(Wed) 10:48)
その通りですね.間違えていました.
Re: スカラーポテンシャルによる場の表示
toorisugari no Hiro さんのレス (2007/10/31(Wed) 13:04)
yamaさん,followありがとうございます. くやしいから:-)考えてみました.
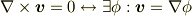
という問題ではなく,
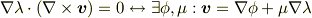
という問題だったのですね. 勉強になりました.
Re: スカラーポテンシャルによる場の表示
まぴお さんのレス (2007/10/31(Wed) 14:35)
toorisugari no Hiroさん,yamaさんありがとうございました. 今回のことでスカラーポテンシャルのことが,だいぶわかりました. やっぱり付焼刃ではだめですね.しっかりと電磁気学を勉強したいと 思います.
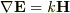 の式は正しいのですか?
の式は正しいのですか?
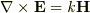 の間違いではないのですか?
の間違いではないのですか?