けん（大学2年） さんの書込 (2007/10/30(Tue) 14:47)

岩波物理入門コース相対性理論p88から一部引用します．

慣性系Sのx軸の正の方向へ速さVで進んでいる慣性系S’を考え，S’の座標をt’=t=0のときSの座標と一致するようにとる． 慣性系Sでx軸の正の方向へ進んでいる平面波を考える． 波動を正弦関数で表し，時空座標の原点における位相が0になるように座標系を定めると，振幅は sin(ωt-kx)…(1) に比例する． 慣性系S’でこの波を観測したときに測定される角周波数をω’，波数をk’とし，(1)と同じ位相の点の時空座標を(x',t')とすれば， ω't'-k'x'=ωt-kx となる．

ここに，ローレンツ変換の式 x=γ(x'+Vt') ct=γ(ct'+βcx') を代入して，振動数の変化を求めています． しかし，上の(x',t')は(1)と同じ位相の点の時空座標として定められており，同じ点であるかは不明です．ローレンツ変換の式を使っているということは位相が同じということから同じ点だと主張するのだと思いますが，どうやって示すのでしょうか．よろしくお願いします．

toorisugari no Hiro さんのレス (2007/10/30(Tue) 19:10)

# これはTeX使う必要ないか．．．

> ローレンツ変換の式を使っているということは位相が同じということから同じ点だと主張するのだと思いますが，どうやって示すのでしょうか．よろしくお願いします．

位相は目に見えづらいものですから，イメージがわきにくいかもしれませんが，スカラー量であることは認めてもらえるでしょうか?

スカラー量なら不変性により同一視できるのでは?

MXK さんのレス (2007/10/30(Tue) 22:41)

たしかに同一の位相の点というのは紛らわしいですね．

同じ時空点Pの系Sでの座標が 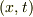, 系S'での座標が 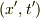と考えるとよいと思います． 系S'での波動が正弦波であることはとくに仮定する必要はなく, 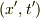で表した波の振幅 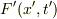が, 系Sでの表式を用いて

と表されるとするべきでしょう．（同一点の振幅は系に依存しない．) これにローレンツ変換の式を代入すると， 系S'の座標で表しても，波は正弦波になっていることが分かり， さらに，その周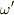波数 , 波数 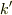が 求められると考えるのが自然だと思います．

けん（大学2年） さんのレス (2007/10/31(Wed) 16:52)

コメントありがとうございます．

＞toorisugari no Hiroさん

スカラーであるかは分かりません．4つの変数により変わる気がします．

＞MXKさん

テキストとは論理が逆になっていますが，これなら納得できます．

＞（同一点の振幅は系に依存しない．)

系に依存しないということまでいえるのでしょうか． テキストでは，sin(ωt-kx)に比例するとなっています．

MXK さんのレス (2007/10/31(Wed) 17:40)

> 系に依存しないということまでいえるのでしょうか．

ここでは 自体がスカラー場(どの系で見ても同じ)であると考えています． この場合，正弦波という制約は不要で，一般の波形に対して

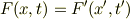
が成り立ちます．(前の記事No.18418のノーテーションを変更しました．) ただ，スカラー場の適当な例がなく，また身近にある電磁場はベクトル場なので， この路線をあきらめて，正弦波の位相をスカラー場と見なそうというのが， toorisugari no Hiro さんや参照されている教科書の立場だと思います． その場合は

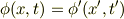
ということになります． 前者の方が概念的にはすっきりしていると思いますが，好みの問題かも知れません．

toorisugari no Hiro さんのレス (2007/10/31(Wed) 17:43)

> 4つの変数により変わる気がします．

位相が変化するなら振幅も変化しますが．．．．

yama さんのレス (2007/11/01(Thu) 08:40)

MXKさんも書かれているようにテキストの記述はあまり適切とはいえず，誤解を招きやすいように思います． 異なる時空点でも位相が等しくなることはあるので，位相が等しいから同一点であるとは言えません． 同一点を考えれば，その位相はどの座標系でも同じであると考えるべきでしょう． 位相が同じであるというのは，たとえば，ある座標系で波の山（または谷）になっている点は，どんな座標系においても波の山（または谷）になっているということです．

toorisugari no Hiro さんのレス (2007/11/01(Thu) 17:12)

確かに，「同じ位置 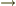同じ位相，だが逆は成り立たない．」ですね．ま，振幅，「山と谷」での区別も本質的におなじ問題をはらんでますが．．．

> (1)と同じ位相の点の時空座標を(x',t')とすれば，
> ω't'-k'x'=ωt-kx
> となる．

そもそも，「同じ点」を位相を使って導く論法が不自然なのですね．(教育的に苦肉の策だというのは認めましょう．)

前提として 「時空の一点という概念は，座標系によらない．(座標系がなくともある質点のあるeventが占める場所時刻は「存在する」)」と考えればいいのではないでしょうか． # 座標系によらず幾何学的点が存在する． # 異なる座標系において，それぞれの座標 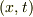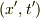， で示される点が同一であるかどうかを，観測によってどう決定するかは不問とします．

そうすれば 「時空内のある点Pを考える．ある座標系を考え，Pの時空座標を 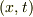とする．この座標系で観測される波数と角速度を 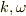とする．

別の座標系を考える．点Pの時空座標を 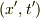，この座標系で観測される波数と角速度を 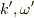とする．

位相 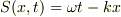はスカラ場だから同一点の値は座標系によらない．すなわち，

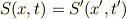
が成り立つ．

よって 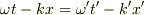となる．」 と自然にかけますよね．(位相の変わりにスカラ正弦波の振幅 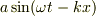でやってもいいですが．．．) (位相がスカラ場であることは．．．振幅を異なる座標系で観測することから導かれる．．．でもいいけどa prioriにしましょう．)

もっとも，「座標系によらず幾何学的点(or 幾何学的対象)が存在する．」はプレ相対性原理みたいなもので，初学者にこれを認めさせるのはつらいかな?

けん（大学2年） さんのレス (2007/11/05(Mon) 11:33)

みなさまご説明ありがとうございます．

＞yamaさん おかげさまで位相のイメージができました．

＞MXKさん 論理的な説明できちんと理解できました．ありがとうございます．

＞toorisugari no Hiroさん ＞位相がスカラ場であることは．．．振幅を異なる座標系で観測することから導かれる．．．でもいいけどa prioriにしましょう． a priori というのはなぜスカラー場なのかを導くのではなく，「そう定義する」くらいの意味なのでしょうか．辞書にはいろいろ書いてありますが．

toorisugari no Hiro さんのレス (2007/11/05(Mon) 13:51)

>> 位相がスカラ場であることは．．．振幅を異なる座標系で観測することから導かれる．．．でもいいけどa prioriにしましょう． > a priori というのはなぜスカラー場なのかを導くのではなく，「そう定義する」くらいの意味なのでしょうか．辞書にはいろいろ書いてありますが．

そうです．「先験的」くらいの意味ですか．相対論で決定するのではなく，その前の(古典力学や波動論の)観測や考察で「単色波の山谷は座標系によらない」つまり「位相はスカラである」とわかっている(信じている)くらいのニュアンスです．

ですから，「位相がスカラ場であることは．．．仮定にしましょう．」と読んでください．

けん（大学2年） さんのレス (2007/11/06(Tue) 11:59)

スカラ場としてしまって困ったことが起きなければスカラ場としてしまっていいではないか．っていう物理ではよくある話のことですね．わかりました．ありがとうございました．

toorisugari no Hiro さんのレス (2007/11/06(Tue) 12:48)

> スカラ場としてしまって困ったことが起きなければスカラ場としてしまっていいではないか．っていう物理ではよくある話のことですね．

身も蓋もない言い方:-)ですが，全くその通りです．

位相がスカラーかどうか，古典的な波動論では成り立つことはわかっても，特殊相対論でなりたつか，一般相対論で成り立つか，重力場の量子論でなりたつか，だれもわかりません．

ですから仮定するわけです．

仮定を立て，理論を組み立てます．そして，理論の論理体系に齟齬がおきたり，実験結果をうまく説明できなかったときは「デバッグ(バグ取り)」をして，仮定に問題があることがわかれば，それを修正する(できなければ捨てる)． というのが現代物理の考え方です． (もちろん，それ以前に仮定が自然か?シンプルで美しいか?といった「審美眼」でも判定しますが．．．)