テーラー展開

ソードさんの書込 (2007/10/30(Tue) 13:31)

大学1年生のソードと言います．

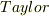Taylor 展開についての質問です．

，は十分小さい場合に以下の式が成り立つ．

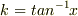
$k=tan^{-1}x$

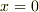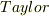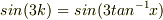
ここで， x=0 について以下の式を Taylor 展開するという問題です． $sin(3k)=sin(3tan^{-1}x)$

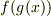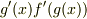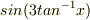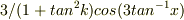自分で考えたことは，合成関数 f(g(x)) の微分は， g'(x)f'(g(x)) なので $sin(3tan^{-1}x)$ の微分は， $3/(1+tan^{2}k)cos(3tan^{-1}x)$ で良いのでしょうか？

解き方の方針でもいいので教えて下さい．

# tan -> tan, sin -> sin , cos -> cosとするときれいですよ．

>  |e0ec29abcc0445b9aa9272302553f29b| の微分は， |d0b7daeda54313fb029ea4f200d93000| で良いのでしょうか？

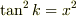$\tan^{2} k = x^2$ とすればいいですね．そもそも，何次まで求めるのでしょう．

私なら，微分せず $\tan(3\tan^{-1}x)$ をの有理式に変換してから考えますが．．．

さらに

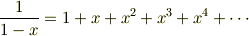
$\frac{1}{1-x} = 1+x+x^2+x^3+x^4+\cdots$

をつかうと $\tan(3\tan^{-1}x)$ をの級数に展開できます．