微分方程式
微分方程式
じゃこび さんの書込 (2007/10/30(Tue) 12:09)
微分方程式についての質問です.少し修正しました.
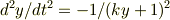
 は定数で,
は定数で, 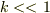
 において
において 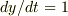 ,
, 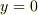
 において
において 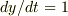 との条件から
との条件から
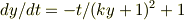
ここからの解き方が解りません.
よろしくお願いします.
Re: 微分方程式
toorisugari no Hiro さんのレス (2007/10/30(Tue) 19:37)
> 条件から > dy/dt = 1 - t/(ky+1)2 > ここからの解き方が解りません.
この式は意味不明です.微分しても与式になりません. この式はどこから出たのでしょうか?
# たぶん「正しい」やり方は,エネルギー積分の手法で一回積分し,変数分離形に持っていくものだと思いますが...根号のはいった有理式の積分はつらい...
Re: 微分方程式
じゃこび さんのレス (2007/10/30(Tue) 22:43)
内容に間違いがあり直しました. 大変申し訳ありません.
訂正後も,エネルギー積分の手法でしか解けないでしょうか? よろしくお願いします.
Re: 微分方程式
toorisugari no Hiro さんのレス (2007/10/30(Tue) 22:48)
TeXで書いてもらってうれしいです.
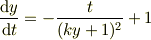
この式を微分しても,
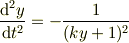
にはなりません.何故ならば, 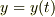 だからです.
だからです.
# 正直,このような躓き方をしている方にはこの問題(問題は間違ってませんか?)は荷が重いと思います.かなり,難しい部類の問題だと思います.
Re: 微分方程式
なんとなく さんのレス (2007/10/31(Wed) 01:20)
じゃこびさん,初めまして,なんとなくです.
Hiroさんの言われることは尤もだと思いますが,出題の背景や本人の事情もあることでしょう.TEXでなくて申し訳ないですが,横レスでHint.を書きます. <Hint.> (1)与式のky(t)+1=ξ(t)と変数変換し,次式を得る. ξ''+k/ξ^2=0(以下,微分を'で表す) (2)両辺にξ'を掛けると, ξ'ξ''+kξ'/ξ^2=0 これは, d/dt{(ξ')^2/2-k/ξ}=0 と書けるので,{・・}は定数C(tによらない) ∴(ξ')^2/2-k/ξ=C(これが一回積分してあり,エネルギー積分です) このCは初期条件から決定できます. (3)上式は一階微分方程式であり,どの教科にもよく出ている変数分離法で解けま す. Hiroさんの言われた根号の積分が少し面倒ですが,公式集であたればいいでしょう.ここまでが理解できれば,あとは自力でできると思います.頑張って.