電気と磁気について

電気と磁気について

しーに さんの書込 (2007/10/29(Mon) 17:51)

始めて投稿します．しーにです．よろしくおねがいします．

早速質問ですが，コイルとコンデンサからなる回路では コイルとコンデンサの間でキャッチボールのようなものが起こると習い その周期をT＝２π√LCと答えられるとあるのですが，よく意味がわかりません． そもそもキャッチボールのようになってるという様子が頭の中に浮かびません．

出典はわかりませんが，どうかお願いいたします．

Re: 電気と磁気について

toorisugari no Hiro さんのレス (2007/10/29(Mon) 18:01)

> コイルとコンデンサの間でキャッチボールのようなものが起こる

「コイルとコンデンサの間でエネルギーのキャッチボールが起こる」 ですね．

単振動において 「質点とバネの間でエネルギーのキャッチボールが起こる」 という言葉が理解できるのなら，そのようなものだとおもえばいいです．

そして ある量を蓄えるものは何か? ある量の変化を嫌うものは何か? で，どれとどれがおなじ働きをするかを考えてみてください．

単振動でもイメージできないなら，単振動のエネルギー保存則をもう一度勉強されてはどうでしょう．

Re: 電気と磁気について

しーに さんのレス (2007/10/29(Mon) 18:53)

お返事ありがとうございます．自分でも少し考えてみました． 質点とバネの間でのエネルギーとはつまり，位置エネルギーと運動エネルギーのことですか？

その場合上から強く押すことで位置エネルギーが消失し，変わりに運動エネルギーが蓄えられるということですね． 考えてみてわからなかった点とは変化を嫌うものというところです．

これはつまりバネがもとに戻ろうとする力いわば反発力（復元力でしたか？）と呼ばれるものなのでしょうか？

Re: 電気と磁気について

toorisugari no Hiro さんのレス (2007/10/29(Mon) 19:28)

# No.18391少し変更しました．

> 考えてみてわからなかった点とは変化を嫌うものというところです．

質量をもつものは慣性の法則により速度の変化を嫌います．速度を変化させるには「力」が必要で，「力」は「慣性質量」に比例します．

コイルは磁束の変化，すなわち，電流の変化を嫌います．電流を変化させるには「電圧」が必要で，「電圧」は「自己インダクタンス」に比例します．

Re: 電気と磁気について

クロメル さんのレス (2007/10/30(Tue) 01:17)

はじめまして，しーにさん．

私は高校の浪人中に，この現象を微分方程式（回路方程式）で扱うことを 学んで大きな感銘を受けたので，ちょっと書いてみます．

スイッチとコイルとコンデンサーが直列につながっている回路を考えます． コンデンサーには，電荷がたまっていてスイッチを閉じると放電します．

コンデンサーで起こる電圧降下は，電流の上流側に溜まっている正電荷の量を qと置く（これは符号の定義：負の電荷が溜まっているなら，q<0とすればいい）と，

V_C=q/C

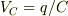
コイルで起こる電圧降下は，上流から下流へ流れる時，正の電流が流れるということにすると(i>0)，

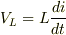
V_L=L\frac{d i}{dt}

ですね．

ここで注意しておくとここで電圧降下といったのは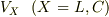， V_X\ \ (X=L,C) の値が正ならば上流に比べて下流の電位が低いからです．

ここで，回路方程式を立てると， （電源電圧）＝（回路の電圧降下）より，

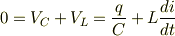
0 =V_C+V_L=\frac{q}{C}+L\frac{di}{dt}

これでは，なんだか分かりませんよね． しかし，この回路には 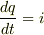\frac{dq}{dt}=i という関係があるんです．

よって，この二式からiを消去して，Lで割って適当に移項すると，

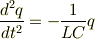
\frac{d^2 q}{dt^2}=-\frac{1}{LC}q

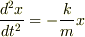
この方程式は，ばね振動子（調和振動子）の方程式と同じ形をしています． \frac{d^2 x}{dt^2}=-\frac{k}{m}x

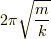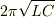この方程式の解の振動周期は， 2 \pi \sqrt{\frac{m}{k}} ですから， これに対応する回路の周期は， 2 \pi \sqrt{LC} となります．

これを文章で説明してみます．

コンデンサーは抵抗のない導線でつなぐと瞬間的に放電します． しかし，その導線にコイルを入れると，コイルは電流変化率に比例した電圧を 変化を妨げる方向に生じますので，急激な変化はできなくなり，徐々に放電がおこります．

コンデンサーは放電して電圧を下げていくので，いつまでも電流は増加しません．電流が最大値を取った後は，今度はコイルは変化を妨げる方向，つまり電流が減少しないように電圧を生じます．徐々に電流が小さくなっていくわけです．

電流が０になったとき，今度はコンデンサーには，符号が逆の電荷が溜まっている状態になり，今度は符号を変えて同じようにコンデンサーが最初の状態に戻るまで，電流が逆方向に流れます．

これはコンデンサーの静電エネルギーとコイルの磁気エネルギーでエネルギーのキャッチボールをしていると言えます．

長文失礼しました．

Re: 電気と磁気について

しーに さんのレス (2007/10/30(Tue) 06:20)

布団の中で考えてたら寝ちゃってました． 返事が遅れて申し訳ないです． クロメルさんとtoorisugari no Hiroさんのおかげでやっと理解できました！ 丁寧な説明ありがとうございました！

また質問に来るかもしれないのでその時またはお願いいたします．

Re: 電気と磁気について

クロメル さんのレス (2007/10/30(Tue) 23:49)

だらだらと書いてしまった気がしたので，言いたいことが伝わったか心配でしたが，手伝えてよかったです．

それでは，また．