直流電源のＬＣＲ並列回路
直流電源のＬＣＲ並列回路
サンダーＳＰ さんの書込 (2007/10/29(Mon) 00:48)
こんばんは．また質問，というより解けないので教えてください．
以下分かりやすく図示できるよう，直交座標を導入します．O(0,0),A(1,0),B(2,0),C(0,1),D(1,1),E(2,1)として，線分OB,CE,OC,AD,BEは全て導線でつながっており，OCに起電力E0の内部抵抗0の直流電源Ｗ(C側が+)があるとします．次にCD間に抵抗Rの抵抗ＸとスイッチＳを，AD間に自己インダクタンスLのコイルＹを，帯電している電気量0の静電容量CのコンデンサーＺを接続します．（つまり，Y,Zは並列，Y,Zをひとまとめにしたものと，Z,Wは直列）
また，Ｙを流れる電流をIy，Ｚを流れる電流をIz(共に，Wの起電力の向きと一致)とし，Ｚの帯電している電気量をQ(E側が正)とすると，キルヒホッフ則より，
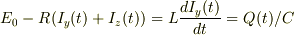で，tで微分し，
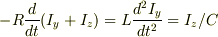となると思うのですが，この微分方程式がどうしても解けません．
初期条件はあまり考慮しておりませんが，簡単な考察では，Zの電圧が0より，Yにすぐに電流は流れず，Iy=0で，Iz=E0/RとなりZの電圧が増加し，同時に，Iy+Izが減少かつ，Iyが増加で，Izが急速に減少し，ついには負になって・・・ と分からなくなります．（dIy/dtはt=0で不連続でしょうか？）
複素インピーダンスは交流で無いので使えませんし，解をフーリエ級数やべき乗級数の和として考えてもみましたが，数学的技量の不足もあってか，解けませんでした． あと確認としての質問ですが，電源の電圧の関数が正弦波以外のときは，様々な正弦関数の和として考え，電流は，各分解した正弦関数に対応する電流の重ね合わせとして考えても良いのでしょうか？ 長ったらしい質問文ですが，お願いいたします．
Re: 直流電源のＬＣＲ並列回路
yama さんのレス (2007/10/29(Mon) 08:52)
左側の＝の式と，右側の＝の式に分けて考えると，2番目の式の右側の式より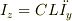 
になるので，これを最初の式の左の式に代入すると 
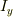だけの方程式になると思います．
Re: 直流電源のＬＣＲ並列回路
サンダーＳＰ さんのレス (2007/10/29(Mon) 19:09)
ありがとうございます． 今教えられると，そうか，と納得して気が抜け，今考えてみれば，なんでこんなのが解けなかったのかと思うくらい恥ずかしい問題でした．（でもこれに２時間半費やしてしまったのも事実です．）
ちなみにこれを解いた所，計算を間違えてなければ少し面白い解が得られました．
