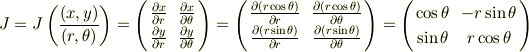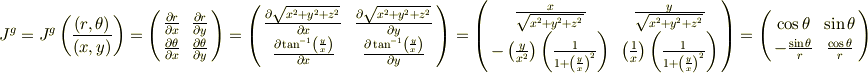Jacobi行列について

Jacobi行列について

リッチ さんの書込 (2007/10/26(Fri) 04:41)

おはようございます． 今Jacobi行列について考えているのですが，ご教授願いたいと思います．

x=rcosθ，y=rsinθについて， そのJacobi行列（ラウンドx/ラウンドr，ラウンドx/ラウンドθ，ラウンドy/ラウンドr，ラウンドy/ラウンドθ）を求めよ．そしてその逆変換のJacobi行列を求めよ． （行列が上手く表せなかったので順に11成分，12成分，21成分，22成分を表していると思ってください）

これなのですが，前者が（cosθ，-rsinθ，sinθ，rcosθ），後者が前者の行列式がrとなり原点を除き可逆となるので，求めるものは前者の逆行列である1/r(rcosθ，rsinθ，-sinθ，cosθ）になると思うのですが，これであっておりますでしょうか？

よろしくお願いいたします．

Re: Jacobi行列について

スパイク さんのレス (2007/10/26(Fri) 11:33)

一応導出過程を出しておきます．

J=J\left(\frac{(x,y)}{(r,\theta )}\right)=\left(\begin{array}{@{\,}cc@{\,}} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta } \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta }\end{array} \right)=\left(\begin{array}{@{\,}cc@{\,}} \frac{\partial (r\cos \theta )}{\partial r} & \frac{\partial (r\cos \theta )}{\partial \theta } \\ \frac{\partial (r\sin \theta )}{\partial r} & \frac{\partial (r\sin \theta )}{\partial \theta }\end{array} \right)=\left(\begin{array}{@{\,}cc@{\,}} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{array} \right)
J^{g}=J^{g}\left(\frac{(r,\theta )}{(x,y)}\right)=\left(\begin{array}{@{\,}cc@{\,}} \frac{\partial r}{\partial x} & \frac{\partial r}{\partial y} \\ \frac{\partial \theta }{\partial x} & \frac{\partial \theta }{\partial y}\end{array} \right)=\left(\begin{array}{@{\,}cc@{\,}} \frac{\partial \sqrt{x^{2}+y^{2}+z^{2}}\, }{\partial x} & \frac{\partial \sqrt{x^{2}+y^{2}+z^{2}}\, }{\partial y} \\ \frac{\partial \tan ^{-1}\left(\frac{y}{x}\right)}{\partial x} & \frac{\partial \tan ^{-1}\left(\frac{y}{x}\right)}{\partial y}\end{array} \right)=\left(\begin{array}{@{\,}cc@{\,}} \frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}\, } & \frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}\, } \\ -\left(\frac{y}{x^{2}}\right)\left(\frac{1}{1+\left(\frac{y}{x}\right)^{2}}\right) & \left(\frac{1}{x}\right)\left(\frac{1}{1+\left(\frac{y}{x}\right)^{2}}\right)\end{array} \right)=\left(\begin{array}{@{\,}cc@{\,}} \cos \theta & \sin \theta \\ -\frac{\sin \theta }{r} & \frac{\cos \theta }{r}\end{array} \right)

＃結果は合っています．

Re: Jacobi行列について

リッチ さんのレス (2007/10/26(Fri) 20:53)

yama様，迅速に有難うございました． スパイク様，ご丁寧に導出過程を掲載して頂きどうも有難うございました．つかえていたことが解消しとても助かりました．心より感謝申し上げます．