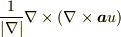波動方程式

まぴおさんの書込 (2007/10/24(Wed) 15:14)

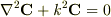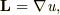
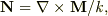
以下の方程式（ヘルムホルツ方程式というのでしょうか？）を解く論文を読んでいて，疑問がありましたので投稿させていただきました． $\nabla^{2}{\bf C}+{\it k}^{2}{\bf C}=0$ 論文にはscalar spherical wave ${\it u}$ を使うと，次の3種類のベクトル球面波がベクトル関数についての基底関数の完全系を作ると書かれてあります． ${\bf L}=\nabla{\it u},$ ${\bf M}=\nabla\times{\bf a}{\it u},$ ${\bf N}=\nabla\times{\bf M}/{\it k},$ ${\bf a}$ は任意の定ベクトル「なぜこの3つが突然出てきたのか？」，また「なぜこの３つで完全系になるのか」？よくわかりません．電磁気学をあまり勉強したこともなく，的の外れた質問かもしれませんが，どうぞよろしくお願いいたします．

Re: 波動方程式

toorisugari no Hiro さんのレス (2007/10/24(Wed) 15:47)

$\nabla u$ と $\nabla \times \bm{a}u$ と $\frac{1}{|\nabla|}\nabla \times (\nabla \times \bm{a}u)$

が一次独立ですか．．．．

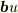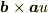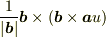$\bm{b} u$ と $\bm{b} \times \bm{a}u$ と $\frac{1}{|\bm{b}|}\bm{b} \times (\bm{b} \times \bm{a}u)$ が一次独立なのは自明ですが，ベクトル演算子だとちょっとやっかいですね．

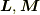$\bm{L},\bm{M}$ が直交する事は自明ですが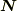， $\bm{N}$ がこれらと一次独立なのは今はわかりません．

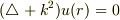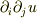あと，scalar spherical waveの性質を書いてください． # $(\triangle + k^2) u(r) =0$ と予想して書いてます． # 特に $\partial_i \partial_j u$ がわかるとうれしいです．

P.S. 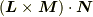$(\bm{L}\times\bm{M})\cdot\bm{N}$ を計算すれば

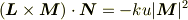
$(\bm{L}\times\bm{M})\cdot\bm{N} &= -ku |\bm{M}|^2$

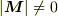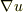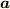となるので $|\bm{M}|\ne 0$ ( $\nabla u$ が $\bm{a}$ と平行でない)ならば一次独立ですね．

Re: 波動方程式

まぴおさんのレス (2007/10/24(Wed) 16:16)

ありがとうございます．ひょっとすると，何か条件があるのかもしれません．少し調べてみたいと思います．

ところで，初歩的な質問ですが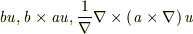， ${\it bu},{\it b}\times{\it au},\frac{1}{\nabla}\nabla\times\left({\it a}\times\nabla\right){\it u}$ が一時独立なのは自明なのですか？外積をとっているので，なんとなくそうなのかなとはわかりますが，よろしければもう少し教えていただけると助かります．

よろしくお願いいたします．

Re: 波動方程式

toorisugari no Hiro さんのレス (2007/10/24(Wed) 16:25)

> ところで，初歩的な質問ですが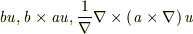， > ${\it bu},{\it b}\times{\it au},\frac{1}{\nabla}\nabla\times\left({\it a}\times\nabla\right){\it u}$ が一時独立なのは自明なのですか？

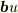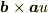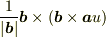$\bm{b} u$ と $\bm{b} \times \bm{a}u$ と $\frac{1}{|\bm{b}|}\bm{b} \times (\bm{b} \times \bm{a}u)$ が一次独立についてですか?

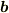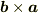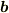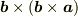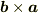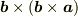$\bm{b}$ と $\bm{b} \times \bm{a}$ とは外積の性質により直交しますね．同様に $\bm{b}$ と $\bm{b} \times (\bm{b} \times \bm{a})$ ，および， $\bm{b} \times \bm{a}$ と $\bm{b} \times (\bm{b} \times \bm{a})$ とは直交しますね．

Re: 波動方程式

スパイクさんのレス (2007/10/24(Wed) 18:44)

補足させて頂くと，

この場合，楕円型ポアソン方程式となりまして，

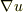
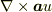
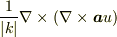$\nabla u$ $\nabla \times \bm{a}u$ $\frac{1}{|k|}\nabla \times (\nabla \times \bm{a}u)$ が直交する事を用いています．＃第一成分のみでいいので，確認されたら宜しいかと思います．＃第二・三成分については，成分を入れ替えるだけになります．

道具立てです♪（根気良くやれば出ます）

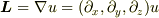
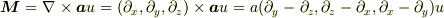
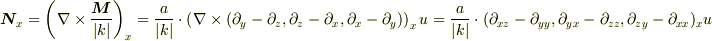
$\bm{L}=\nabla u=(\partial _{x},\partial _{y},\partial _{z})u$ $\bm{M}=\nabla \times \bm{a}u=(\partial _{x},\partial _{y},\partial _{z})\times \bm{a}u=a(\partial _{y}-\partial _{z},\partial _{z}-\partial _{x},\partial _{x}-\partial _{y})u$ $\bm{N}_{x}=\left(\nabla \times \frac{\bm{M}}{\left|k\right|}\right)_{x}=\frac{a}{\left|k\right|}\cdot \left(\nabla \times (\partial _{y}-\partial _{z},\partial _{z}-\partial _{x},\partial _{x}-\partial _{y})\right)_{x}u=\frac{a}{\left|k\right|}\cdot (\partial _{xz}-\partial _{yy},\partial _{yx}-\partial _{zz},\partial _{zy}-\partial _{xx})_{x}u$

＃大事なのは，境界条件によって解がどの様になることかと，思われます．

)参考になれば，幸いです． *)添字・太字の誤記を訂正しました．

Re: 波動方程式

まぴおさんのレス (2007/10/24(Wed) 21:50)

toorisugari no Hiroさん，スパイクさんありがとうございました．すっきりしました．

toorisugari no Hiroさん，No.18323の質問は頭がボーっとしててとんでもない初歩的な質問をしてしまいました．

また何かあるときはよろしくお願いします！

[home] [掲示板] [ページの先頭]