外積の分配法則
外積の分配法則
あきら さんの書込 (2007/10/24(Wed) 11:29)
外積には分配法則が成立します. 物理の本では,大抵,幾何的な定義をしたあと,単位ベクトルを用いた成分の計算法が書かれています.しかし,ここでは暗黙のうちに分配法則が使われています. 簡単に自明とはいえないと思うのですが,証明はどうするのでしょか?
初めから成分で定義して,それから幾何的な納得をするのがいいのでしょうか?
分配法則の証明方法または,すんなりとした外積の導入法を知りたいです. よろしくお願いします.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 11:52)
しんくろにしてぃー?
質問が重なってますが,気にせずに...
> しかし,ここでは暗黙のうちに分配法則が使われています. > 簡単に自明とはいえないと思うのですが,証明はどうするのでしょか?
外積をどう導入するかに依存します.  で定義して,成分に置き換え,線形性を導入するのも手ですし,
で定義して,成分に置き換え,線形性を導入するのも手ですし,
成分で定義するのも手ですし,
角度も成分も使わず,最初から,線形性と反交換性を公理として,外積を導入すれば,「備え付け」です.
今,時間がないので,最後の手法に興味があれば,いってください.後で,説明します.
Re: 外積の分配法則
あきら さんのレス (2007/10/24(Wed) 13:20)
ありがとうございまうす. そこまでは,ぼくも同感です.
ぼくは,高校生に外積を教えるときに,シンプルな導入方法はないかと考えています.
>absinθで定義して,成分に置き換え, そう思うのですが,これは正面から証明するにはかなり手間がかかりますよね. 結局,結果を示して,これが大きさ,方向ともに外積の幾何的な定義を満たしていることを示して終わりになってしましました. 般教の力学の教科書では,大抵分配法則は,自明としているようです.
>最初から,線形性と反交換性を公理として,外積を導入すれば,「備え付け」です. そのとおりです.ただ,これを行うと, 「外積ってめんどう」と思われて「フレミングの方がいいや」 って思われると思います. 内積と外積の数学的な(テンソル的な)深い意味はあとで知ればいいことと思います.
外積の便利さは,幾何的な定義と分配法則から発生していると考えてるのですが,その部分をシンプルに示す方法はないでしょうか?
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 14:46)
> 外積の便利さは,幾何的な定義と分配法則から発生していると考えてるのですが,その部分をシンプルに示す方法はないでしょうか?
素直に,
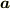 と
と 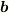 が作る平行四辺形の面積と
が作る平行四辺形の面積と 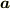 と
と  が作る平行四辺形の面積とを足したものは
が作る平行四辺形の面積とを足したものは 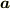 と
と 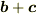 が作る平行四辺形の面積に等しいことを幾何学的に証明するのではダメですか?
が作る平行四辺形の面積に等しいことを幾何学的に証明するのではダメですか?
# もっとも,これが自明に見えるのは2次元に限定されますが.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 15:13)
気になったのですが,高校生に「3次元」の外積ですか? 2次元ならともかく,3次元はさすがに,無理だと思うのですが....
Re: 外積の分配法則
あきら さんのレス (2007/10/24(Wed) 16:28)
2次元の外積の意味がわかりません,,, 外積はいつも3次元ですよね. なんかぼくが勘違いしてるのかな.
磁場からの力を扱うときには,参考書や塾では外積で扱ってると思います. 教科書には書いてありませんが.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 16:33)
ごめんなさい. もう一つのスレッドと混同してしまいました. #ベクトル積関連が3個あるのは.... 以下の話は無視してください.
2次元では外積は定義できないのでしょうか?
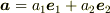 ,
, 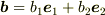 ,
, 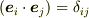 としたとき
としたとき
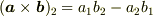 ですよね?
ですよね?
もちろん(z成分が0の)3次元ベクトルと考えるなら,
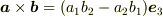 ですが.
ですが.
あ,説明されていないんで,わからなかったんですが,もしかして高校生ですか?
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 17:04)
> 2次元の外積の意味がわかりません,,, > 外積はいつも3次元ですよね. > なんかぼくが勘違いしてるのかな.
> 磁場からの力を扱うときには,参考書や塾では外積で扱ってると思います. > 教科書には書いてありませんが.
この世は3次元だから2次元を考えるのは意味がないということなら,おっしゃるとおりです.でも,2次元に制限された運動を考えるときや複素解析とベクトル解析の関係を考えるときには2次元も意味があるし,ですから,2次元の外積も意味があると思うのですが.
なにより,外積のおおまかな性質を理解するにはまず2次元の外積からと,私は思います.
# そして3次元では面積でなく体積を先に考えて,そこから面積ベクトルを導入する考え方が好きです.(教育効果は置いておくとして)
Re: 外積の分配法則
yama さんのレス (2007/10/24(Wed) 17:25)
横から失礼します.
外積を成分で定義すれば分配法則は簡単に導かれるので,成分で定義してから幾何学的意味を考えるといいのではないでしょうか. これについては次の記事が参考になると思います.
この記事の中では,外積がもとのベクトルに直交することと,その大きさが平行四辺形の面積に等しいことが論じられています.
Re: 外積の分配法則
あきら さんのレス (2007/10/24(Wed) 17:44)
toorisugari no Hiroさん おそらく話がすれ違ってますよね. 外積とは,かける二つのベクトルに垂直な方向なので,2次元では定義できない と考えています.それに,フレミング左手の法則は3次元ですよね. でも,きっとtoorisugari no Hiroさんが言っていることは違いそうです. なにかぼくが勘違いしていそうですね.
yamaさん ぼくも,結局成分で定義するのが,面倒なようで早道のように感じ始めています. やっぱり,座標軸というものは強力なものですね.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 17:51)
そもそも,私は外積とは反対称テンソルであるという立場です.3次元でのみ(擬)ベクトルとしてあつかえるというだけで,外積はベクトルであるとはおもっていません.
ですから,2次元の外積も矛盾なく定義できると思っています.
Re: 外積の分配法則
あきら さんのレス (2007/10/24(Wed) 18:06)
言っていることはわかります. 勿論テンソルまでいかないと,内積と外積の対応は納得できませんよね.
ただ,磁場からの力を書くのに2次元の外積をどう用いるのか ぼくには,わかりません.
Re: 外積の分配法則
s さんのレス (2007/10/24(Wed) 18:17)
確か昔の学習指導要領では3次元での平面の扱いからベクトルの外積のさわりと ,それの簡単な応用まで入っていたような. 教え方さえ間違えなければ高校生に教えるのは決して無理ではないと思いますよ.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 18:26)
> ただ,磁場からの力を書くのに2次元の外積をどう用いるのか > ぼくには,わかりません.
ああ,そういう意味ですか.当然,2次元の外積は3次元の力学の記述に「直接」は関係しません.
もっとも,3次元外積 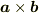 は,2つのベクトルで張られる平面の単位法線ベクトル
は,2つのベクトルで張られる平面の単位法線ベクトル 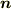 に,平面内における2次元外積
に,平面内における2次元外積 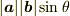 をスカラー倍したもの(
をスカラー倍したもの( 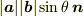 )と定義すれば,使えなくはないですが,成分式や線形性の導出に負担は来ますね.
)と定義すれば,使えなくはないですが,成分式や線形性の導出に負担は来ますね.
そこら辺になると,教え方の問題(成分から入るか?角度から入るか? 2次元を説明して3次元にいくか?)ですね.
Re: 外積の分配法則
yama さんのレス (2007/10/24(Wed) 21:33)
2次元の外積の例としては,平面上の力のモーメントがあります. 高校で扱う剛体の釣り合いの問題では,ほとんどの場合,力は1平面(XY平面)上にあります. 従って3次元的に考えると,力のモーメントはz成分だけになってしまいますが,成分が1つだけなので,その値をもつスカラー(正確には擬スカラー)を2次元の外積と考えることができるでしょう. 高校物理の教科書では,力のモーメントは3次元ベクトルとしては扱われず,実質的に2次元の外積として扱われているように思われます.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 22:06)
元々の問題に戻りますが,線形性は導くものではなく,最初から要求される性質だと思います.
面積や体積などの測度は加算性が本質的です.(重複しないふたつの図形の測度はそれをあわせた図形の測度に等しいし,逆に一つの図形の測度はそれを分解した図形の測度の和に等しい.)
測度の加算性を認めると,ベクトルの組み合わせで作られる平行四辺形の面積や平行六面体の体積は,各辺をなすベクトルに対して線形であることはユークリッド幾何学の作図から導かれます.
よって線形性の要求は当然だと思います.
# もちろん教え方は自由です.線形性を後から導くやり方でも問題はないと思います.
# 面積の線形性を認めれば,必然的に面積は符号を持つ量になります.ですが,積分 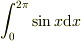 を考えると面積に正負があることは自然だと思えます.
を考えると面積に正負があることは自然だと思えます.
Re: 外積の分配法則
あきら さんのレス (2007/10/24(Wed) 23:08)
定義をしてからの議論でないと すれ違いに,なっていると思います.
面積をなんとなく外積と語ってしまうと,交換則まで成立しているように, 間違いそうです.
体積は内積も含んでいますし,,,, ぼくが分かっていないせいだと思いますが,前提を説明していただきたいです.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/24(Wed) 23:13)
> 面積をなんとなく外積と語ってしまうと,交換則まで成立しているように,間違いそうです.
もちろん,面積の交換則はなりたちません.
2次元ベクトル 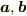 で張られる平行四辺形の面積
で張られる平行四辺形の面積 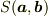 の反交換則
の反交換則
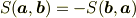
が成り立つことは
(1) (双)線形性
(2) 平行な(一次従属な)ふたつのベクトルで作られる面積は0である.
ことを要求すれば導かれます.
# 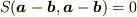 から出ますね.
から出ますね.
# この性質から面積は2階の反対称テンソルであることが出てきます.さらに,2次元面積は2階の「完全」反対称テンソルであることもわかります.
体積 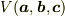 が奇置換に対して符号反転することも同様に導かれます.(ここからスカラー三重積の性質が導き出されるのであって,逆ではないです.)
が奇置換に対して符号反転することも同様に導かれます.(ここからスカラー三重積の性質が導き出されるのであって,逆ではないです.)
# この性質から体積は3階の「完全」反対称テンソルであることが出てきます.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/25(Thu) 00:17)
> 前提を説明していただきたいです.
とても高校生には見せられない衒学的バージョンでいきます.
2次元の外積 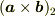 とは,ふたつの2次元ベクトル
とは,ふたつの2次元ベクトル 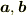 で張られる面積
で張られる面積 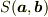 であり,完全反対称テンソル量です.(内積が定義されているときはこれは擬スカラ量
であり,完全反対称テンソル量です.(内積が定義されているときはこれは擬スカラ量  になります.)
になります.)
3次元の体積 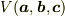 は完全反対称テンソル量です(内積が定義されているときはこれは擬スカラ量
は完全反対称テンソル量です(内積が定義されているときはこれは擬スカラ量 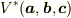 になります).内積が定義されているときは,体積の第一変数に対する擬スカラ線形関数
になります).内積が定義されているときは,体積の第一変数に対する擬スカラ線形関数 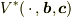 は擬ベクトル量と同一視できます(リースの表現定理 Riesz representation theorem).これが「面積」であり,これを3次元の外積
は擬ベクトル量と同一視できます(リースの表現定理 Riesz representation theorem).これが「面積」であり,これを3次元の外積 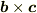 と定義します.
と定義します.
つまり,内積が定義されると,  となるようなベクトル
となるようなベクトル 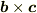 が導入でき,双線形反対称な性質を満たすことから,これを「面積」とみなせるという話です.
が導入でき,双線形反対称な性質を満たすことから,これを「面積」とみなせるという話です.
# 3次元の場合,体積と内積が定義されてはじめて,外積ベクトルが定義できます.スカラー三重積から外積が定義されるというのがおもしろいです.なお,内積が定義されていないとき外積は2階の反対称テンソル量です.
# 完全反対称テンソルを擬スカラー量と見なすのに内積が定義されている必要があるか,ちょっと自信ないです.ほかにもいろいろ穴があります.気が付いたら指摘してください.>識者の方
# 前提の前提としては,私は外積はまず,幾何学量として定義され,そこから代数的性質が導かれると考えています.もちろん,代数的性質を先に定義して,そこから幾何学へ導く考え方もあるでしょう.
Re: 外積の分配法則
スパイク さんのレス (2007/10/25(Thu) 13:03)
こんにちは♪
>完全反対称テンソルを擬スカラー量と見なすのに内積が定義されている必要があるか,ちょっと自信ないです.
完全反対称テンソルが擬スカラー量となる場合には,内(外)積が定義されている必要があります.(1)
一般に /* 『内(外)積が定義できる幾何(空間)では,完全反対称となるテンソルが存在する』(2) */ とすれば,判っている方には,通じやすいかと思います.
#擬スカラーは,一般にはスカラー密度を指しますので,スカラー(テンソル)とは,区別したほうが宜しいかもしれません.
外積の場合には,絶対値を取ることによって,スカラー(量)積を求めているというべきかもしれません.
#何らかの実例か応用例をやってみると,馴染んでくるかと思われます. /* */の箇所のみ訂正としておきます(擬スカラーとスカラーの関係).
*)疑問点がある場合には,ご質問下さい.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/26(Fri) 08:37)
やっぱり,きちんとテンソル積や双対空間からやらないと,計量に依存しない外積の議論は厳しいみたいです.
計量いれる見返りに線形代数の知識を援用した版に変更します.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/26(Fri) 08:38)
No.18342,No.18345の変更版です. もはやチラシの裏です.
以下,内積(計量)が定義されている実ベクトル空間に限定する.よって,正規直交基底 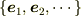 を使うことができ,また,「角度」や「距離」を使うことができる.
を使うことができ,また,「角度」や「距離」を使うことができる.
I. 2次元面積
[* 基本的性質 *]
2次元平面内のベクトル 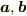 の張る平行四辺形の面積
の張る平行四辺形の面積 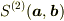 は以下の性質をもつことが幾何学から要請される.
(a) 双線形性 (
は以下の性質をもつことが幾何学から要請される.
(a) 双線形性 ( 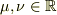 )
)
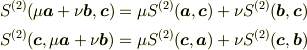
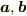 が一次従属(共線)
が一次従属(共線) 
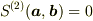
このとき,次の性質が導かれる.
(b') べき零性 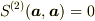 (
( 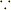 (b))
(b'') 反対称性
(b))
(b'') 反対称性 
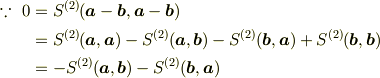
つまり,2次元面積は構成するベクトルに対して双線形で「完全」反対称な量である.
# 完全反対称とは置換に対して反対称な変化をする要素の組の大きさが,空間の次元と一致することである.今の場合,2組の2次元ベクトルが反対称なので,完全反対称である.
[* 成分表示 *]
いま,正規直交基底  を用いて
を用いて  ,
, 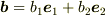 とおくと,
とおくと,
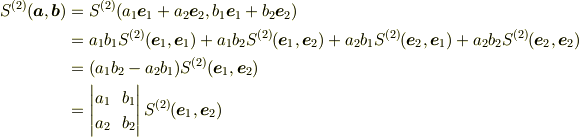
となる.
[* 極座標表示 *]
極座標表示 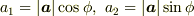 ,
, 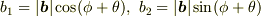 を使えば
を使えば
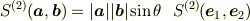
が得られる.
[* 擬スカラ性 *]
2次元面積は一個の2次元面積「基底」(  面積の単位)
面積の単位) 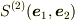 のみで記述されることがわかる.これは「完全」反対称性の帰結であり,2次元面積の『スカラ』性を示唆している.
のみで記述されることがわかる.これは「完全」反対称性の帰結であり,2次元面積の『スカラ』性を示唆している.
2次元面積基底 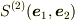 は
は 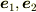 で張られる「単位正方形」の面積であるから,
で張られる「単位正方形」の面積であるから, 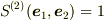 と採るのが自然であるように思われる.
と採るのが自然であるように思われる.
その考察は基底の回転
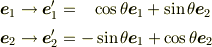
を行っても,回転の行列式は1であることより,
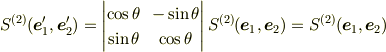
となり,値が不変,つまり『スカラ』量と考えられることからも支持される. (どの「単位正方形」の面積を基準にとってもかまわない.)
しかし,反転変換で状況が変わる.反転を含む変換 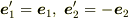 によって得られた新しい正規直交基底
によって得られた新しい正規直交基底 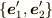 でおなじ論理を展開させても,「自然」な根拠から,
でおなじ論理を展開させても,「自然」な根拠から, 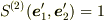 となる.しかし,これは
となる.しかし,これは  を意味し,線形性により矛盾となる.
を意味し,線形性により矛盾となる.
この原因は面積が空間反転でスカラ量と符号が異なる変換をする「擬」スカラ量であることによる.
空間反転を含まない直交座標変換で結ばれる基底に限れば,面積基底の値は同一なので, 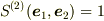 と置くことができる.
と置くことができる.
II. 体積
[* 基本的性質 *]
3次元空間内のベクトル 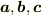 の張る平行六面体の体積
の張る平行六面体の体積 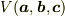 は以下の性質をもつことが幾何学から要請される.
(a) 多重線形性 (
は以下の性質をもつことが幾何学から要請される.
(a) 多重線形性 ( 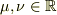 )
)

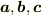 が一次従属(共面)
が一次従属(共面) 
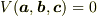
このとき,Iと同様に次の性質が導かれる.
(b') べき零性 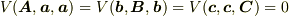 (b'') 反対称性
(b'') 反対称性
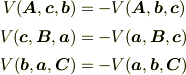
(b''') 循環性  (
( 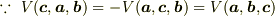 )
)
つまり,体積は構成するベクトルに対して多重線形で完全反対称な量である.
[* 成分表示 *]
いま,正規直交基底 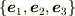 を用いて
を用いて
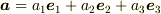 ,
,
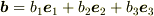 ,
,
 ,
とおくと, Iと同様に
,
とおくと, Iと同様に

となる.
[* 擬スカラ性 *]
体積は一個の体積「基底」 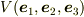 のみで記述されることがわかる.これは完全反対称性の帰結であり,体積の『スカラ』性を示唆している.
のみで記述されることがわかる.これは完全反対称性の帰結であり,体積の『スカラ』性を示唆している.
3次元回転(行列式=1)による正規直交基底の変換に対して体積基底 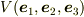 の値が変わらないことと,体積基底
の値が変わらないことと,体積基底 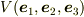 は
は 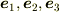 で張られる「単位立方体」の体積であることから,
で張られる「単位立方体」の体積であることから, 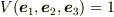 と採るのが自然であるように思われる.
と採るのが自然であるように思われる.
しかし,Iと同様に反転に対して 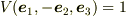 という矛盾が起こることから,体積も「擬」スカラ量であることがわかる.
という矛盾が起こることから,体積も「擬」スカラ量であることがわかる.
体積をスカラ量と考えるためには,空間反転を含まない座標変換,あるいは「右手系」「左手系」でグループ化された正規直交基底類の中での成分表示,を行わなければいけない.そのときは 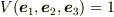 と考えて良い.
と考えて良い.
III. 3次元面積(1)
[* 基本的性質 *]
3次元空間内のベクトル 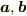 の張る平行四辺形の面積
の張る平行四辺形の面積 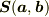 について考察する.2次元面積との類推から,以下の性質が要請されることは自然と思われる.
(a) 双線形性 (
について考察する.2次元面積との類推から,以下の性質が要請されることは自然と思われる.
(a) 双線形性 ( 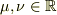 )
)
 が一次従属(共線)
が一次従属(共線) 
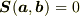
このとき,Iと同様に次の性質が導かれる.
(b') べき零性 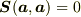 (b'') 反対称性
(b'') 反対称性 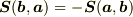
つまり,3次元面積は構成するベクトルに対して双線形で反対称な量である.
[* 成分表示 *]
いま,正規直交基底 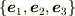 を用いて
を用いて
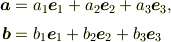
とおくと,

となる.ただし,

である.
[* ベクトル基底 *]
2次元面積は一個の「基底」のみで記述されたが,3次元面積は3個の「基底」 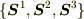 で記述される.これらが一次独立であることは性質(b)から導けるので,3次元面積は『ベクトル』の性質をもつ.
で記述される.これらが一次独立であることは性質(b)から導けるので,3次元面積は『ベクトル』の性質をもつ.
IV. 3次元面積(2)
[* 基本的性質の追加 *]
前節IIIにより3次元空間内のベクトル  の張る平行四辺形の面積
の張る平行四辺形の面積  がベクトル的性質を持つことが示唆された.しかし,「基底」
がベクトル的性質を持つことが示唆された.しかし,「基底」 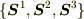 と正規直交基底
と正規直交基底 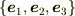 との関係が不明である.そこで,従来の要請
(a) 双線形性 (
との関係が不明である.そこで,従来の要請
(a) 双線形性 ( 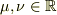 )
(b)
)
(b) 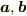 が一次従属(共線)
が一次従属(共線) 
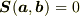 に加え,新しい性質
(c) (体積=高さ×底面積)
に加え,新しい性質
(c) (体積=高さ×底面積) 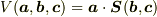 を要請する.
を要請する.
性質(c)と体積の反対称性により以下の性質が導出される.
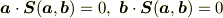
すなわち,面積ベクトル 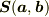 はベクトル
はベクトル 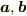 にともに垂直,すなわち
にともに垂直,すなわち 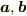 が張る平面の法線に平行である.
が張る平面の法線に平行である.
[* 面積基底と正規直交基底 *] 性質(c)により

が得られ,これと基底の完全性の条件(ただし, 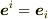 とする.)
とする.)
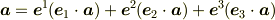
と併せて,
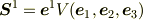
以下同様に

が得られる.
[* 擬ベクトル性 *]
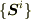 は
は 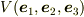 をふくんでいるので,反転では
をふくんでいるので,反転では 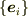 と異なる符号の変化をする.その意味で
と異なる符号の変化をする.その意味で 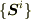 は擬ベクトルである.しかし,右手系に基底を限定すれば
は擬ベクトルである.しかし,右手系に基底を限定すれば 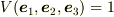 なので,
なので, 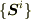 は
は 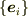 に一致し,
に一致し,
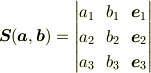
と表示できる.
- まとめ
多重線形性と,「測度と一次独立性の関係」を仮定すれば,2次元面積,体積の擬スカラー性が,および,3次元面積の『ベクトル』性が導ける.さらに体積と面積の関係を仮定すれば,3次元面積が擬ベクトルであることが導かれる.
Re: 外積の分配法則
toorisugari no Hiro さんのレス (2007/10/27(Sat) 16:50)
# 3次元面積がベクトルであることを線形性を公理に出すにはだしましたが,苦しい.
外積に線形性があることをどう導くかには,外積とは何かをよく考えないといけないと思います.
外積とは 幾何における面積である. 反対称テンソルの演算の翻訳である. 3個の数字の組に対する「反対称な積」の性質を持つ代数計算である. 電磁気学や力学における,ベクトル間の「積」の性質をもつ2項演算子である. 電磁気学の式を簡潔に表現(イメージ)する単なる技法である.
これらは一つのものの側面にすぎないですが,本質(テンソル)は結構やっかいなのでなかなか統一的にとらえられません.個別にやっていくしかないでしょう.
たとえば,電磁気関連(角運動量関連)で外積を導入するのなら,線形性は物理から要求されることです.成分で定義して線形性が「導出」されたとしてもそれは「確認」にすぎません.線形性はそもそも「物理の要請」で最初から存在してるのです.
「磁場や電場はベクトル」といった時点で,線形性は「備え付け」なのです.ベクトル間をつなぐ演算が線形でなれば磁場や電場は「ベクトル」ではなく,単に「向きと大きさと方向」を持つ量(  ベクトル)にすぎません.
ベクトル)にすぎません.
もちろん,教え方の問題は別です.厳密にやっても生徒にわかってもらえないので,誤解を承知で,「まず,理解してもらうこと」は大事です.
でも,それなら,たとえば,角度をつかって,外積を 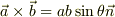 から定義して,その後計算により線形性を導くよりも,定義したあと,別口で(簡単な物理的考察で)線形性をつけくわえる方がよいと,私は,思います.
から定義して,その後計算により線形性を導くよりも,定義したあと,別口で(簡単な物理的考察で)線形性をつけくわえる方がよいと,私は,思います.
ともかく,教え方を工夫されたいのなら,一度,きちんと全体像を把握されることをおすすめします.以下の本は「ベクトル」をより深く理解したい人に向いてます.
SGCライブラリ 39 「マクスウェル方程式」〜 電磁気学のよりよい理解のために 〜 北野正雄著