Terry さんの書込 (2007/10/24(Wed) 03:21)

ベクトルについて教えてもらえませんか？ ベクトルaとbについて， a・bは|a||b|cosθのスカラーで， a×bは大きさが|a||b|sinθのベクトル と習いました． なんで内積はスカラーになって，外積はベクトルになるのですか？ 教えて下さい．

逆に，a・bが|a||b|cosθのベクトルで a×bが|a||b|sinθのスカラーじゃまずかったんでしょうか？

toorisugari no Hiro さんのレス (2007/10/24(Wed) 11:11)

> なんで内積はスカラーになって，外積はベクトルになるのですか？ 教えて下さい．

ううううむ．難しい質問です．Terryさんが満足する様な答えはたぶんできません． 「世界がそうなってるから」というのが一番近いかもしれません．

でも，それではなんなので，意味を探ることで少しでも理解できればと思って説明します．

まず内積，これは，ある意味外積より難しいのですが，えいやーーと，「射影」と理解することにしましょう．ふたつのベクトル 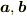があるときに，片方のベクトル 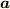にもう一方のベクトルの影 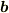を映します．影のながさ 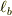にベクトル 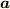の長さ をかけたものを，内積

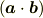
と呼びます．いま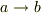， の順番でしたが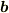， に 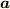の影を落として計算した結果もおなじ事は幾何で証明できます．長さと長さのかけ算ですからスカラです．

射影という言い方がわからないなら，「相関」でもいいです．ふたつのベクトルがどれだけ重なり合うか，どれだけ平行かの度合いが内積と理解してもいいです．

相関をそれぞれのベクトルの大きさで割ったものが相関係数で，相関係数が 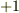なら順平行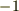， なら逆平行， なら，つまり無相関なら，直交とよびます．当然おわかりかと思いますが，相関係数は 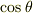です．

相関は重なり合ってるか，そうでないか示す量です．また，この考えは2次元空間でも3次元空間でも4次元以上の空間でも同様にできなければいけません．なので，スカラーでなければいけないのは納得いただけるでしょうか?

外積は，ページがないので次ぎにします．

toorisugari no Hiro さんのレス (2007/10/24(Wed) 11:44)

> なんで内積はスカラーになって，外積はベクトルになるのですか？

外積が何故ベクトルになるかですが，一般に外積はベクトルではありません． # 内積は何次元でもスカラーですが．．．

2次元では外積は(擬)スカラーです． 3次元では外積は(擬)ベクトルです． 4次元以上では外積はスカラーでもベクトルでもない，テンソルと呼ばれるものになります．

#「(擬)」は気にしないでいいです．

何で，こんな事になるかというと，外積はふたつのベクトルが作る平行四辺形の「面積」だからです．

ふたつのベクトルが作る平行四辺形を考えましょう．この平行四辺形を指定すれば，面積は決まります．つまり，面積は平行四辺形を指定する事に依存します．

平行四辺形を指定するためには，その辺をなす，ふたつのベクトルを指定しなければいけません．このとき，「平行四辺形」(正確には面積)はふたつの方向を持つ量であることに注意してください．

大きさと一つの方向で指定される量を「ベクトル」というのを発展して，ふたつ以上の方向で指定される量を「テンソル」といいます．ま，行列みたいなものです．

ただ，テンソルという量は扱いづらいので，スカラーやベクトルに「翻訳」したいと考えるのが人情ですが，2次元と3次元のときは可能です．

3次元では，ふたつのベクトルの組み合わせでできる平行四辺形はいろいろな方向をもちます．方向を指定するには，2個のベクトルを指定しなければいけないのは先ほど言いましたが，面に垂直な方向で「代用」できることに気づくはずです．

空間は3次元なので，2個のベクトルで張られる平面を，2個のベクトルで指定もできますし，平面に垂直なベクトルで指定すること(1次元)もできます．１＋２＝３というわけです．

それで，本当は外積はベクトルではないのですが，代用してベクトルと考えます．

2次元では0+2=2なので，2個のベクトルで張られる平面は方向は固定です．ですから，面積を単にスカラーで考えてもよいのです．あるいはxy平面を考えるとき，外積はz方向をもつベクトルなのだが，方向は不変なのでz成分だけで代用すると考えても良いです．

外積は平行四辺形の面積です． 2次元では面積は符号(向き)のみを持つ量です(積分計算において，面積に符号があると便利なのは知ってますよね)． 3次元では面積は方向をもちます．方向をいれることで，面積の足し算が矛盾なくできます．(詳細は省きます．興味があれば質問してください．)

でも，本当は，面積はテンソルなのです．ただ，3次元では，ベクトルでかんがえられるというだけです．

冗長になってしまいました．．．．．．．．

Terry さんのレス (2007/10/25(Thu) 03:41)

ありがとうございます．

外積が面積だってことも理解できました． たしかに底辺が|b|で高さが|a|sinθの平行四辺形の面積ですね． 外積は，「平行四辺形がどの平面かも特定でき，さらに大きさも表せる」ってことでベクトル(←テンソル？)なんですね．

内積も外積も「積」という字がついていて「掛け算」というイメージでしたが， ベクトルの射影の求め方が「内積」という方法で， 面積＋面積の方向(平面)の求め方が「外積」という方法なのですね． こういう計算方法を作り出すことによってどんな役に立つのかは今後勉強するとして，内積・外積の概念はわかりました．

ちなみにテンソルっていうのは，図で表すと矢印(ベクトル)ではないってことなのでしょうか． ん〜・・・上手く表現できないのですが，代用してベクトルで表せるならベクトルなのではないかと・・・・

全体的に理解できました． 丁寧に長文で回答していただいてありがとうございます．

toorisugari no Hiro さんのレス (2007/10/25(Thu) 12:37)

理解してくださってうれしいです．

> 外積は，「平行四辺形がどの平面かも特定でき，さらに大きさも表せる」ってことでベクトル(←テンソル？)なんですね．

3次元では，ですね．:-) 直線に平行なベクトル(「接ベクトル」といいます)というのはイメージしやすいのですが，平面に垂直なベクトル(「法ベクトル」といいます)はなかなか理解しづらいものです．まして，面積が符号を持つだけでなく方向をもつというのも感覚的に受け入れられないものがあると思います．

物理の例を調べてたり，いろんな問題を考えたり，本を読むなどして，イメージを身につけてください．

> 内積も外積も「積」という字がついていて「掛け算」というイメージでしたが，

線形性(分配則やスカラー倍に関する演算)がなりたつことが積といってるだけなので(「双線形な2項演算子を積とよぶ」がより正確ですが．．．．)，数のかけ算と混同しないようにしなけばいけませね．

> ちなみにテンソルっていうのは，図で表すと矢印(ベクトル)ではないってことなのでしょうか．

面積テンソルに限定すれば，平面内の矢印付きの円(角度が増える方向を矢印でしめす．)でもいいです．

例えば半径 の矢印付きの円によって，面積の大きさが 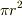で示されるといったかんじですね．方向も自然にわかりますよね．

これは3次元ベクトルではありません．ただし，普通はさらに「右ねじの法則」によりベクトル(ねじが進む方向3-2=1)で代用してしまいますが．

# ちなみに4次元空間だと「矢印付きの円」が4次元空間に浮かんでいるのは理解できると思いますが，もうベクトルで代用できません( )

今回納得されたと言うことですが，元々の > 逆に，a・bが|a||b|cosθのベクトルで > a×bが|a||b|sinθのスカラーじゃまずかったんでしょうか？ という疑問はそのまま考え続けられた方がよいと思います．

内積がベクトルだと不都合はないか?(2次元，3次元，4次元で矛盾は起きないか?)(足し算に矛盾は起きないか)など考えるのは勉強になると思います．(もちろん受験勉強優先ですが)

もしかしたら，新しい数学を発見できるかしれませんよ．