やす さんの書込 (2007/10/19(Fri) 12:56)

トルクの単位は[N・m]だと言われます．この単位は次元的にはエネルギと同じで[N・m]=[J]です．それが，どうにも腑に落ちないのです．また，回転している軸のトルク（T=P/ω）と，トルクレンチで締め付けたとき均衡して動いていないときのトルクは同じものでしょうか？

やす さんのレス (2007/10/19(Fri) 14:52)

質問の補足：軸に糸を巻きつけて，おもりを1m持ち上げたとすると，おもりの位置エネルギは確かに増えます．この場合の位置エネルギは，持ち上げるのに要した時間に関係ないはずです．このエネルギを要した時間で割れば[J/s]=[W]で，（平均的な）P（仕事率）は求まる（対応が付く）ような気もします．そうすると，P/ω[W/s^(-1)]=[Ws]で表わせるトルクとは何なのでしょうか？

toorisugari no Hiro さんのレス (2007/10/19(Fri) 16:09)

> トルクの単位は[N・m]だと言われます．この単位は次元的にはエネルギと同じで[N・m]=[J]です．それが，どうにも腑に落ちないのです．

トルク×角度がエネルギーに相当する量なので，本当は違うのですが，角度radが無次元なのが悩ましいですね．次元的にはおなじだが，本質は違うものと考えた方がよいと思います．

ｙama さんのレス (2007/10/19(Fri) 17:00)

toorisugari no Hiroさんが書かれた通りですが，具体例で補足しておきます． 軸に糸をまきつけておもりを持ち上げる場合，軸の半径をr，回転角度をθとすると，おもりははrθだけ引き上げられます． 糸の張力をFとすると，このときの仕事は力Fと移動距離rθの積，すなわちFrθです．これはトルクFrと回転角度θの積でもあります． すなわち，トルクと回転角度の積が仕事（またはエネルギー）に等しいわけです． 角度は無次元量なので，トルクとエネルギーの単位は同じになります．

やす さんのレス (2007/10/19(Fri) 17:49)

技術的な（現場での）公式では ωTのωは[rad/s]（ω=2πf[rad/s]）で，[rad]という訳では無いのですが，これでωT=P[W]と合うことは合うのですが．

MXK さんのレス (2007/10/19(Fri) 19:54)

直線運動の場合の 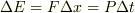に 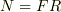, 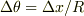を 代入したもの 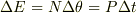が今問題になっている式ですね．( はエネルギ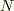， はトルク, は半径) 2つの式から出てくる 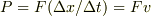と 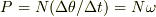を比較すれば，何か分かるのではないでしょうか．

yama さんのレス (2007/10/19(Fri) 22:27)

ω[rad/s]は角速度なので，回転角度θ[rad]を時間[s]で割ったものです． トルク×回転角度＝仕事 の両辺を時間で割れば トルク×角速度＝仕事率（すなわちωT=P） になります．

rammstein さんのレス (2007/10/21(Sun) 12:24)

まったく理論的でない意見ですみません．銀河を回転運動させている中心で 回転面にたいしてジェットが垂直に吹き出しているのをみると トルクはエネルギ？って印象になったりします．