静電容量

キャロットさんの書込 (2007/10/15(Mon) 23:08)

暑さ２ｄ，面積Ｓの平行平板コンデンサの極番間に，誘電率がＸの関数として ε＝ε0*3d/(2X+d)で変化する厚さｄの誘電体をはさんだ．静電容量を求めなさいという問題なのですが，どういう風に解いていっていいのかわかりません… どなたかお願いします

蓄えられる電荷をQとして，ガウスの法則を利用して極板間の電束密度Dを求めると，DはXに無関係な一定値になることが分かるでしょう．極板間の電場E=D/ε はXの関数になるので，それを積分することによって極板間の電位差

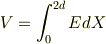
$V=\int_0^{2d}EdX$

を計算することができ，従って Q=CV の関係から静電容量Cが求められます．

ということはこの場合 0→d で積分し d→2dで積分したものをたして電位差を求め，c=Q/φで解いたらよいのでしょうか？ φ＝∫σ/ε・dx ＋∫σd/ε0・dx

誘電体の厚さを2dと思い込んでいましたが，dでしたね．その場合，積分は誘電体のある区間と誘電体のない区間の積分の和になるので，キャロットさんの式で計算すればいいと思います．ただし第2項は∫σ/ε0・dx（=σd/ε0）ですね．

わかりました，どうもありがとうございました