サイクロイド,微分方程式
サイクロイド,微分方程式
けん(大学2年) さんの書込 (2007/10/15(Mon) 11:53)
2yy"+y'^2+1=0 の解が x=a(t-sint) y=a(1-cost)(aは任意定数) で表されることは,微分方程式に代入すれば分かります. ・2階微分の方程式なので,任意定数はもう1つ必要だと思うのですが,どこに入れればいいのでしょうか ・解が分かっていない場合,解析的に解けるのですか?
よろしくお願いします.
Re: サイクロイド,微分方程式
yama さんのレス (2007/10/15(Mon) 12:19)
「'」はtについての微分を表しているのでしょうか? そうだとするとy=a(1-cost)は微分方程式を満たしていないように思われます. また微分方程式にxが含まれていないので,その微分方程式からは,xは定まらないと思います. xを含む微分方程式が他にあるのではないでしょうか?
Re: サイクロイド,微分方程式
スパイク さんのレス (2007/10/15(Mon) 14:06)
けんさん,yamaさんこんにちは.
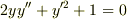 ,
, 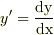
<サイクロイド>
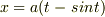
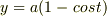 (
( 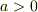 は任意定数)
は任意定数)
>・2階微分の方程式なので,任意定数はもう1つ必要だと思うのですが,どこに入れればいいのでしょうか
線形微分方程式の場合には,任意定数がもう一つ必要ですが,この方程式の場合には, (その自由度を)媒介変数表示に用いているようです.
と思ったら,ありました♪
<トコロイド>
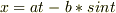
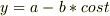 (
( 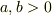 は任意定数)
は任意定数)
<エビ・トコロイド>
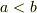
<ハイポ・トコロイド>
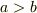
さて,微分方程式をうまく満たしているでしょうか?
*)サイクロイドは, 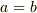 の場合
の場合
>・解が分かっていない場合,解析的に解けるのですか?
非線形の場合には,保証はありません.従って,解法を成書にまとめておいたのでしょう. #定理・公式の類は,そのような場合が多いかと思います.
*)微分方程式から,日常生活の範囲で解を想定するのは,一つの手かもしれません?
Re: サイクロイド,微分方程式
toorisugari no Hiro さんのレス (2007/10/15(Mon) 16:25)
> 任意定数はもう1つ必要だと思うのですが,どこに入れればいいのでしょうか
 を回転する円の角度だとすれば,初期位相
を回転する円の角度だとすれば,初期位相  がそれに当たりますね.
がそれに当たりますね.
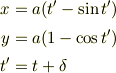
( 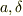 は任意定数)
は任意定数)
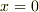 のときの角度
のときの角度  (初期位相)は任意のはずです.
(初期位相)は任意のはずです.
Re: サイクロイド,微分方程式
yama さんのレス (2007/10/15(Mon) 16:32)
なるほど,「'」はxについての微分を表すのですね.それなら話は分かります. 電磁場中の荷電粒子の軌道がトロコイドになる場合がありますが,その場合の運動方程式からtを消去すればけんさんが書かれた微分方程式になるのでしょうね. 従って適当な変数変換によってtを含む運動方程式の形にすることができるとは思いますが,その変換を見つけるにはいろいろ試行錯誤するしかないように思います.
Re: サイクロイド,微分方程式
toorisugari no Hiro さんのレス (2007/10/15(Mon) 16:44)
> 従って適当な変数変換によってtを含む運動方程式の形にすることができるとは思いますが,その変換を見つけるにはいろいろ試行錯誤するしかないように思います.
そうですね.ただ,この方程式の場合,各項で 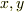 の次数がおなじ(同次形?)ですから,それを頼りに変形はできそうです.
の次数がおなじ(同次形?)ですから,それを頼りに変形はできそうです.
# 今,時間がないので,本を調べられませんが....
Re: サイクロイド,微分方程式
yama さんのレス (2007/10/15(Mon) 16:56)
toorisugari no Hiro さんへ
確かに初期位相は任意なので,私も初めはそれが任意定数ではないかと考えました. しかしよく考えてみると,それはパラメータのとりかたの任意性(の1つ)であって,積分定数としての任意定数ではないと思います. 問題の微分方程式はxとyに関するものであって,tは含みません.tは便宜上導入されたパラメータにすぎません. 微分方程式の解に含まれる任意定数は,その値によってxとyの関係が変化するようなものでないといけません. しかし,初期位相を変えることによってxとtの関係あるいはyとtの関係は変わりますが,xとyの関係は変わりません.
Re: サイクロイド,微分方程式
toorisugari no Hiro さんのレス (2007/10/15(Mon) 17:27)
yamaさん > しかしよく考えてみると,それはパラメータのとりかたの任意性(の1つ)であって,積分定数としての任意定数ではないと思います.
ううむ.そうですね. では,検算していないですが
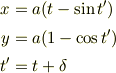
(a,  は任意定数)
ではどうでしょう.(式に
は任意定数)
ではどうでしょう.(式に  は生で出ていませんね.)
は生で出ていませんね.)
Re: サイクロイド,微分方程式
yama さんのレス (2007/10/15(Mon) 21:04)
なるほど,xに任意定数を付加しても微分方程式は変化しないというわけですね.
そうすると確かに 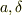 を任意定数と考えてよさそうですね.
あるいは
を任意定数と考えてよさそうですね.
あるいは 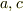 を任意定数として
を任意定数として
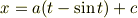
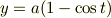
とすることもできますね.
Re: サイクロイド,微分方程式
けん(大学2年) さんのレス (2007/10/16(Tue) 10:39)
yamaさん,スパイクさん,toorisugari no Hiroさん,説明ありがとうございます. y'はxでの微分です.説明不足ですみません.
No.18145のyamaさんの付加定数をはじめに考え,先生に聞いてみたのですが, yをxの関数として表すのだから,xに定数を付加しても意味はない と言われてしまいました….
Re: サイクロイド,微分方程式
toorisugari no Hiro さんのレス (2007/10/16(Tue) 10:44)
> xに定数を付加しても意味はないと言われてしまいました….
ははは.
ま,前提の問題でしょう. # No.18136にかんしてはそのとおりですが.
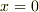 のとき
のとき 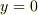 と決められていれば
と決められていれば 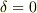 です.
です.
でも,一般にはそうとは限りませんね.
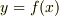 が題意の微分方程式をみたすなら,
が題意の微分方程式をみたすなら,
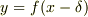 も題意の微分方程式をみたします.
も題意の微分方程式をみたします.
関数形だけが重要というなら,先生の意見も納得できますが...
Re: サイクロイド,微分方程式
toorisugari no Hiro さんのレス (2007/10/16(Tue) 15:21)
一応,導出してみますね.予定調和的なのはご勘弁
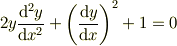
 を
を
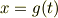
と置いてみます.そうすると
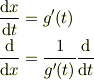
これを代入すると
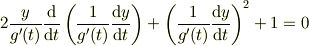
ここで
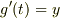 ,すなわち
,すなわち
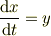
および,
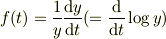
とおくと
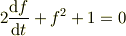
さらに
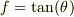 とすれば
とすれば
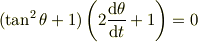
これより,
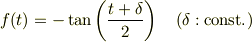
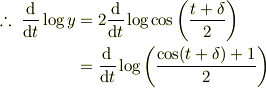
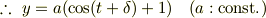
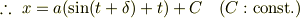
ただし, 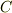 は
は  をshiftして
をshiftして  に繰り込むことで消せる.(あるいは逆に
に繰り込むことで消せる.(あるいは逆に  を消せる.)
を消せる.)
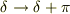 とすれば
とすれば
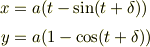
Q.E.D.
Re: サイクロイド,微分方程式
なんとなく さんのレス (2007/10/16(Tue) 18:26)
けんさん,こんにちは.なんとなくです.
横レス,失礼します. yamaさんの?18145は正しいと思い,媒介変数を使わず解いてみました. 2yy''+y'^2+1=0('はxについての微分)・・・? さらにxで微分して,整理すると, y^2y''=c(cは任意定数)より,y''=c/y^2.これと?を比較して y'^2=c/y-1 これは1階微分方程式で変数分離形で解け, ∫√y・dy/√(c-y)=∫dx 積分して整理すると,被積分関数=tan(θ)と置いて, x=c/2(2θ-sin(2θ))+c',y=c/2(1-cos(2θ))(c'は任意定数) ここで,c/2→a,c'→b,2θ→θと読み替えると, x=a(θ-sin(θ))+b,y=a(1-cos(θ)) と所定の結果が得られます.任意定数の置き方は他にもあるでしょうが,同値であり,正解だと思います...
サイクロイド,微分方程式
けん(大学2年) さんのレス (2007/10/22(Mon) 11:22)
>toorisugari no Hiroさん 導出ありがとうございます. 導出ですが,dx/dtをyとおけるのはどうしてでしょうか.yはx(あるいはt)の関数であるというだけでyがどのような関数形かはまだわかっていません.
>なんとなくさん 式変形を追うことができました.ありがとうございます.
Re: サイクロイド,微分方程式
toorisugari no Hiro さんのレス (2007/10/22(Mon) 15:17)
> 導出ですが,dx/dtをyとおけるのはどうしてでしょうか.yはx(あるいはt)の関数であるというだけでyがどのような関数形かはまだわかっていません.
 というパラメターを置いたときに
というパラメターを置いたときに 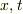 にどのような依存関係があるか未定ですし,任意です.つまり,
にどのような依存関係があるか未定ですし,任意です.つまり, 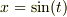 とおこうが
とおこうが 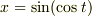 とおこうが論理に影響しません.
とおこうが論理に影響しません.
逆にいうと  は
は  の未定の関数で表されます.つまり
の未定の関数で表されます.つまり 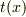 は未定ですし,現段階で任意です.そこで変形した方程式が簡単になるように,
は未定ですし,現段階で任意です.そこで変形した方程式が簡単になるように, 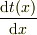 を
を 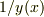 に等しいと仮定したわけです.
に等しいと仮定したわけです.
この操作は 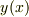 がわかっていなくても問題ありません.
がわかっていなくても問題ありません.