ガウスの定理の証明

むっくさんの書込 (2007/10/15(Mon) 08:07)

課題は，ベクトル場でのガウスの定理は既知としてテンソルS（転値：St）についてガウスの定理を証明するということです．

v；任意のベクトル a：ベクトルa = St・v

体積側のintegrandの計算は以下のように進めました． ∇・a = ∇·(St・v) = (∇·S)·v + S:∇v

ここで右辺第2項がおそらくゼロ（積分することでゼロ？）になると思いますが，理由が解りません．どなたか教えていただけないでしょうか？

お願いします．

$\bm{v}$ は任意ということですが，定ベクトルにしたほうがよいと思います．

この証明には内積の非退化性「任意のベクトル $\bm{v}$ に対して

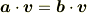
$\bm{a}\cdot\bm{v} = \bm{b}\cdot\bm{v}$

が成り立つのなら

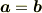
$\bm{a} = \bm{b}$

」を使うのですよね．

ありがとうございます．

私が理解できないことは ∫∇・a dV = ∫∇・（St・v）dV = ∫（（∇・S）・v + S:∇v）dV = 面積分 ↓ v・∫（∇・S）dV = 面積分と証明する中で，S：∇vの項があるため困っています．

この項はゼロなのでしょうか？ゼロでしたら理由を教えていただきたいです．

もう一度繰り返します． $\bm{v}$ は任意ということですが，任意の定ベクトルにしたほうがよいと思います．

そうでないとそもそもNo.18150における下矢印が成り立ちません．