斜面で物体を投げたとき

home > 掲示板 >

このページのPDF版

サイトマップ

斜面で物体を投げたとき

こたさんの書込 (2007/10/14(Sun) 20:04)

こんにちは2度目の質問です．よろしくお願いします．

水平面とβの角をなす斜面の最下点から，斜面とαの角をなす方向に初速ｖ0で物体を投げた．重力加速度はｇとする．

斜面上で測った到達距離Lを求めよ．（斜面をｘ，そこから90度の線をｙ軸とする）また，到達距離Lを最大にするための角αを求めよ．

水平面と角βの角をなす・・というだけで全くわからなくなってしまいます；お答よろしくおねがいします．

Re: 斜面で物体を投げたとき

richiti さんのレス (2007/10/15(Mon) 03:44)

軸方向，軸方向の加速度はそれぞれ $-g\sin\beta$ ， $-g\cos\beta$ なので，の時間変化は

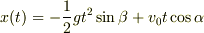
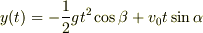
$x(t)=-\frac{1}{2}gt^2\sin\beta+v_0t\cos\alpha$ $y(t)=-\frac{1}{2}gt^2\cos\beta+v_0t\sin\alpha$

と表されます．従って 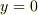y=0 となる時刻は

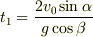
$t_1=\frac{2v_0\sin\alpha}{g\cos\beta}$

となり，これを 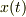x(t) の表式に代入すると

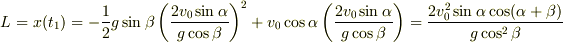
$L=x(t_1)=-\frac{1}{2}g\sin\beta\left(\frac{2v_0\sin\alpha}{g\cos\beta}\right)^2+v_0\cos\alpha\left(\frac{2v_0\sin\alpha}{g\cos\beta}\right)=\frac{2v_0^2\sin\alpha\cos(\alpha+\beta)}{g\cos^2\beta}$

と答えが得られます．

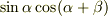次にを最大にする $\alpha$ は $\sin\alpha\cos(\alpha+\beta)$ を最大にするので

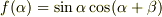
$f(\alpha)=\sin\alpha\cos(\alpha+\beta)$

とおき，導関数をにする $\alpha$ を調べると

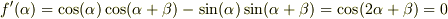
$f'(\alpha)=\cos(\alpha)\cos(\alpha+\beta)-\sin(\alpha)\sin(\alpha+\beta)=\cos(2\alpha+\beta)=0$

なので

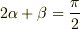
$2\alpha+\beta=\frac{\pi}{2}$

つまり

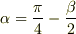
$\alpha=\frac{\pi}{4}-\frac{\beta}{2}$

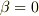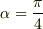となりを最大にする $\alpha$ が求まります． $\beta=0$ のとき $\alpha=\frac{\pi}{4}$ となるのは有名ですね．

[home] [掲示板] [ページの先頭]