ホール効果

ホール効果

三毛猫 さんの書込 (2007/10/13(Sat) 01:39)

はじめまして，理工学部２年のものです．

ホール効果について質問があります．以下の問いについて教えていただきたい次第です．よろしくお願いします．

電子と正孔が濃度n_eとn_pとで存在する． それぞれの平均衝突実感をτ_e，τ_pとし，有効質量をm_e，m_pとする． この系に，磁場B=(0,0,B)，電場E=(E_x,0,0)を印加した．

電子と正孔の運動方程式を求めよ．

電子の運動方程式は， ｘ方向はm d<v_x>/dt = -eE_x -m<v_x>/τ

であると思うのですが，ｙ方向の運動方程式がわかりません． 正孔の方は，考え方がよく分かりません．電子と同じようにすればよいのでしょうか？ご説明をお願いします．

Re: ホール効果

スパイク さんのレス (2007/10/13(Sat) 02:42)

三毛猫さん，こんばんは♪

>ｙ方向の運動方程式がわかりません．

につきましては，まずは，古典的に

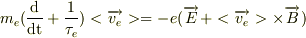
電子の運動方程式: m_e (\frac{\mathrm{d}}{\mathrm{dt}}+\frac{1}{\tau_e})<\overrightarrow{v_e}>= -e(\overrightarrow{E}+<\overrightarrow{v_e}>\times\overrightarrow{B})

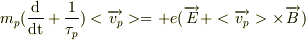
正孔の運動方程式: m_p (\frac{\mathrm{d}}{\mathrm{dt}}+\frac{1}{\tau_p})<\overrightarrow{v_p}>= +e(\overrightarrow{E}+<\overrightarrow{v_p}>\times\overrightarrow{B})

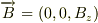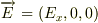
・電子の電荷: e ・印加された磁場: \overrightarrow{B}=(0,0,B_z) ・印加された電場: \overrightarrow{E}=(E_x,0,0)

に従うとして，座標成分毎の方程式を見たら宜しいかとは思われますが，

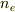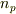>電子と正孔の運動方程式を求めよ． >電子と正孔が濃度 n_e と n_p とで存在する．

と記述されているように，電子と正孔の関係式を加味した方が見通しが宜しいかと思われます．

>正孔の方は，考え方がよく分かりません．電子と同じようにすればよいのでしょうか？

固体物性の場合には，固定化された空孔（電子が抜けた状態）として扱うかと思います． ”抜けた状態”の動きとして見ますので，平均化した上で，密度の変化を見るのが通例かと思われます． まとめると，”電子と正孔の相関を見る”ということです．

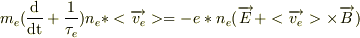
電子の運動方程式: m_e(\frac{\mathrm{d}}{\mathrm{dt}}+\frac{1}{\tau_e})n_e*<\overrightarrow{v_e}>= -e*n_e(\overrightarrow{E}+<\overrightarrow{v_e}>\times\overrightarrow{B})

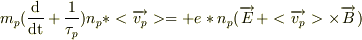
正孔の運動方程式: m_p(\frac{\mathrm{d}}{\mathrm{dt}}+\frac{1}{\tau_p})n_p*<\overrightarrow{v_p}>= +e*n_p(\overrightarrow{E}+<\overrightarrow{v_p}>\times\overrightarrow{B})

で合っているかな？（質量・電荷の保存則を満たすようにすればいいと思います）

＃実例としましては，ホール素子（主に磁場測定に用います）が一般的かと． ＃今，手元にまとまった資料がありませんので，叩き台である事をご了承下さい(^^♪ *）表式は古典論に従っています． *）2007.10.16表式の訂正を行いました．